
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.4. Коэффициент Пуассона
Материал имеет множество параметров: модуль упругости, коэффициент Пуассона, предел текучести, предел временной прочности, плотность, коэффициент линейного теплового расширения, коэффициент теплопроводности и т.п. Каждая характеристика материала, в свою очередь, зависит от условий эксперимента, в частности, от температуры, формы и структуры образца. Поэтому результаты экспериментальных исследований, как правило, носят качественный характер и не в полной мере отражают свойства материала. В этом случае математическое моделирование и численный эксперимент могут дать развернутое представление о характеристиках материала (моно- и поликристаллического, композитного) при проектировании, в частности, рабочих лопаток газовой турбины.
Математическое моделирование и численный эксперимент позволяют существенно сократить объем дорогостоящих экспериментов. В частности, для экспериментов на нитевидных монокристаллах, входящих в состав эвтектических композитов, используется уникальное оборудование. Поэтому моделирование значительно снижает экономические и временные затраты в процессе проектирования элементов авиационных ГТД.
Рассматривается математическая модель расчета коэффициента поперечной деформации (коэффициента Пуассона) n, основанная на электростатической природе упругости.
Коэффициент Пуассона определяется как отношение
n = εy / εx,
где εy – относительная деформация вдоль оси OY; εx – относительная деформация вдоль оси OX.
Математическая модель имеет следующие допущения.
1. Рассматривается бездефектная кристаллическая решетка.
2. По Котреллу [25], разрушение кристаллической решетки происходит при εx = 0,1.
3. Рассматривается область упругой деформации, причем V ≠ const.
4. Максимальное значение коэффициента Пуассона определяется на границе перехода от упругой к пластической области деформации при условии εy = εz и сохранении постоянного объема (рис. 1.31).
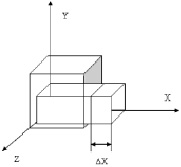
Рис. 1.31. Схема геометрического моделирования поперечной деформации
при продольном растяжении твердого тела
Тогда в исходном состоянии (без нагрузки) при условии x = 1, y = 1, z = 1
V = xyz = 1.
В деформированном состоянии (с нагрузкой)
x1 = x + ∆x; y1 = y – ∆y; z1 = z – ∆z.
Так, при максимальном значении упругой продольной деформации по Котреллу [25] εx = 0,1, максимальное значение коэффициента Пуассона будет равно nмах = 0,47 @ 0,5.
При этом y1 = 0,953y, z1 = 0,953z, тогда
V = xyz = 1,1⋅0,953⋅0,953 = 0,999 @ 1.
Последовательность расчета коэффициента Пуассона для элементарной атомной ячейки бездефектной кристаллической решетки следующая.
При x = y = z = a0 кулоновская сила без нагрузки, т.е. при ∆x = ∆y = ∆z = 0
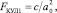
где c = e2 / 4πε0 – коэффициент, e = 1,6·10–19 Кл – заряд электрона; ε0 = 8,85·10–12 Кл2 /Нм2 – электрическая постоянная; а0 – период кристаллической решетки.
Кулоновская сила при поперечном сжатии, т.е. при y1 = 0,953y или 0,953а0 (рис. 1.32)
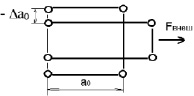
Рис. 1.32. Схема геометрического моделирования поперечной деформации
при продольном растяжении
элементарной атомной ячейки
FКУЛ2 = c / (0,953а0)2.
Изменение кулоновской силы при сжатии
DF = FКУЛ2 – FКУЛ1.
Период кристаллической решетки с учетом изменения кулоновской силы
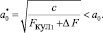
Изменение периода кристаллической решетки с учетом изменения кулоновской силы
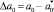
Относительная поперечная деформация после несложных преобразований определяется по формуле [29, 30]
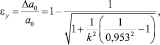
где k = 1 + kстрNорб; kстр – коэффициент, учитывающий тип структуры монокристалла; Nорб – среднее число незаполненных орбиталей внешней электронной оболочки атома.
Тип кристаллической решетки можно определить по справочным данным.
Относительная поперечная деформация
εy = ∆а0 /а0.
Коэффициент поперечной деформации (коэффициент Пуассона)
n = εy /εx = εy /0,1.
Результаты расчетов для некоторых монокристаллических металлов приведены в табл. 1.16.
Таблица 1.16
|
Символ элемента |
Величина коэффициента Пуассона |
||
|
расчетная |
справочная |
погрешность, % |
|
|
Al |
0,33 |
0,36 [31] |
8,3 |
|
Cu |
0,377 |
0,35 [32] |
7,7 |
|
Мо |
0,328 |
0,335 [32] |
2,0 |
|
W |
0,257 |
0,26 [31] |
1,2 |
|
Та |
0,237 |
0,24 [31] |
1,3 |
|
Ni |
0,404 |
0,342* [32] |
18,1 |
|
Fe |
0,308 |
0,3* [32] |
2,7 |
Примечания: значения со звездочкой, приведенные в справочнике, определены расчетом.
Из табл. 1.16, в частности, видно, что расчетное значение коэффициента Пуассона железа Fe равно 0,308, а справочное значение – 0,3.
Выводы
1. Математическая модель расчета коэффициента Пуассона применима для оценки упругих характеристик моно- и поликристаллов, в том числе соединений, по которым редко или совсем не встречается справочная информация.
2. Математическая модель расчета коэффициента Пуассона применима для проектирования эвтектических композитных материалов, используемых в газотурбинных двигателях.
3. Одним из направлений развития нанотехнологий является полное трехмерное управление структурой материалов на атомном уровне с целью размещения каждого атома на своем месте. В этих условиях важно заранее знать упругие и прочностные характеристики нанообъемов монокристаллов с бездефектной структурой. Откуда следует необходимость наличия расчетных формул упругих характеристик, в частности, коэффициента Пуассона.
