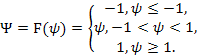Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Моделирование конкуренции в условиях рынка

Степанов Л. В.,

2.3 ВЫБОР ФУНКЦИИ АКТИВАЦИИ И ОБУЧЕНИЕ НЕЙРОННОЙ СЕТИ

Синапсы осуществляют связь между нейронами и умножают входной сигнал на число, характеризующее силу связи - вес синапса. Сумматор выполняет сложение сигналов, поступающих по синаптическим связям от других ней­ронов и внешних входных сигналов. Преобразова­тель реализует функцию одного аргумента, выхода сумматора, в некоторую выходную величину нейрона. Эта функция называется функцией активации нейрона. Нейрон в целом реализует ска­лярную функцию векторного аргумента. В общем случае входной сигнал и весовые коэффициенты могут принимать действительные значения. Вы­ход определяется видом функции активации и может быть как действительным, так и целым. Синаптические связи с положительными весами называют воз­буждающими, с отрицательными весами - тормозящими.

Таким образом,  нейрон полностью описывается своими весами и функцией активации F. Получив набор чисел (вектор) в качестве входов, нейрон выдает некоторое число на выходе.

Активационная функция может быть различного вида [61]. Наиболее широко используемые варианты приведены в таблице (табл.2.1).

Одними из наиболее распространенных функций являются:

• 1. линейная,
• 2. нелинейная с насыщением - логистическая функция или сигмоид,
• 3. гиперболический тангенс.

Линейная функция наилучшим образом соответствует сущности данной задачи.        Ее областью определения является диапазон (-∞, ∞). Это позволяет, используя ценовые характеристики товара на входе, получать характеристические значения любой величины на выходе, равные их фактической сумме.

Следует отметить, что сигмоидная функция (2.12) дифференцируема на всей оси абсцисс, что широко используется во многих алгоритмах обучения.

Таблица 2.1

Перечень функций активации нейронов

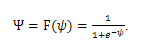                                                                     .                                          (2.12)

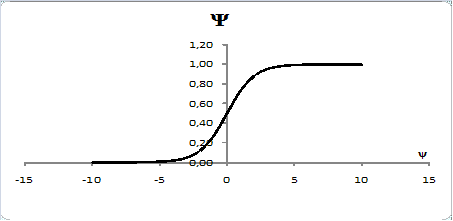
Рис.2.12 Вид сигмоидной функции

Кроме того, она обладает свойством усиливать слабые сигналы лучше, чем сильные, и предотвращает насыщение от сильных сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий на­клон (рис.2.12). Эти особенности важны для задачи моделирования совершенной конкуренции. Рынок совершенной конкуренции характеризуется однородностью, которая заключается в том, что все производители выпускают одинаковый по числу, свойствам и неценовым характеристикам товар. Единственное отличие однотипных товаров разных производителей - это его ценовые параметры. В условиях рыночной экономики отличия ценовых параметров достаточно характерны для рынков товаров и услуг. Однако они, чаще всего, носят не значительный характер. Поэтому разница между однотипными ценовыми параметрами разных товаров, подаваемых на вход нейронной сети, будет невелика, что предъявляет к чувствительности функции дополнительные требования. Нейроны должны «распознавать» слабо различающиеся входные сигналы. Это делает (2.12) наиболее применимой.

В условиях конкуренции участники рынка, производящие или потребляющие товар по очень высоким или по слишком низким ценам, соответственно, не определяют положение дел на рынке. Основными участниками конкурентной борьбы являются предприятия, действующие в области наиболее конкурентоспособной цены. Это обстоятельство вполне соответствует виду функции (2.12).

Другой широко используемой активационной функцией является гиперболический тангенс. В отличие от логистической функции гипербо­лический тангенс принимает значения различных знаков, что для ряда сетей оказывается выгодным.

Важно отметить, что выбор вида активационной функции предлагается осуществлять симметрично в производственном и потребительском сегменте по уровням подсистем. Это обосновывается тем, что производство и потребление товара на рынке являются «зеркальными» процессами и должны протекать по одинаковым принципам. Сам же вид функций определяется исходя из требований точности.

При решении с помощью нейронных сетей задач необходимо собрать достаточный и представительный объем данных для того, чтобы обучить нейронную сеть решению таких задач. Обучающий набор данных - это набор наблюдений, содержащих признаки изучаемого объекта. Нейронные сети работают с числовыми данными, взятыми, как правило, из некоторо­го ограниченного диапазона. В данной задаче эта выборка может быть построена на основе статистической информации, собранной за время существования рынка. Кроме того, количество производителей и поставщиков на рынке совершенной конкуренции достаточно велико и при отсутствии других данных текущие показатели товара могут быть рассмотрены, как обучающая выборка.

Вопрос о том, сколько нужно иметь наблюдений для обучения сети, часто оказывает­ся непростым. Известен ряд эвристических правил, которые устанавливают связь между количеством необходимых наблюдений и размерами сети. Простейшее из них гласит, что количество наблюдений должно быть в 10 раз больше числа связей в сети. На самом деле это число зависит от сложности того отображения, которое должна воспроизводить ней­ронная сеть. С ростом числа используемых признаков количество наблюдений возрастает по нелинейному закону, так что уже при довольно небольшом числе признаков, скажем 50, может потребоваться огромное число наблюдений. Эта проблема носит название "проклятие размерности".

Таким образом, в условиях первого слоя нейронной системы примерное число обучающих примеров можно определить:

                                            μ = w x l x  m.                                                    (2.13)               

Процесс обучения нейронной сети заключается в определении значений весовых коэффициентов, обеспечивающих однозначное преобразование входных сигналов в выходные.

Путем анализа имеющихся в распоряже­нии аналитика входных и выходных данных веса сети автоматически на­страиваются так, чтобы минимизировать разность между желаемым сигналом и получен­ным на выходе в результате моделирования. Эта разность носит название ошибки обучения.

Ошибка обучения для конкретной конфигурации нейронной сети определяется путем прогона через сеть всех имеющихся наблюдений и сравнения выходных значений с желаемыми, целевыми значе­ниями. Эти разности позволяют сформировать так называемую функцию ошибок (крите­рий качества обучения). При моделировании нейронных сетей с линейными функциями активации ней­ронов можно построить алгоритм, гарантирующий достижение абсолютного минимума ошибки обучения. Для нейронных сетей с нелинейными функциями активации в общем случае нельзя гарантировать достижения глобального минимума функции ошибки.

При таком подходе к процедуре обучения может оказаться полезным геометрический анализ поверхности функции ошибок. Определим веса и смещения как свободные пара­метры модели и их общее число обозначим через N; каждому набору таких параметров поставим в соответствие одно измерение в виде ошибки сети. Тогда для всевозможных сочетаний весов соответствующую ошибку сети можно изобразить точкой в N-1-мерном пространстве, а все такие точки образуют некоторую поверхность, назы­ваемую поверхностью функции ошибок. При таком подходе цель обучения нейронной сети состоит в том, чтобы найти на этой многомерной поверхности глобальный минимум.

В случае линейной модели сети и функции ошибок в виде суммы квадратов такая по­верхность будет представлять собой параболоид, который имеет единственный минимум, и это позволяет отыскать такой минимум достаточно просто.

В случае нелинейной модели поверхность ошибок имеет гораздо более сложное строение и обладает рядом неблагоприятных свойств, в частности может иметь локальные минимумы, плоские участки, седловые точки и длинные узкие овраги.

Определить глобальный минимум многомерной функции аналитически невозможно, и поэтому обучение нейронной сети, по сути дела, является процедурой изучения поверхности функции ошибок. Отталкиваясь от случайно выбранной точки на поверхности функции ошибок, алгоритм обучения постепенно отыскивает глобальный минимум. Как правило, для этого вычисляется градиент (наклон) функции ошибок в данной точке, а за­тем эта информация используется для продвижения вниз по склону. В конце концов алго­ритм останавливается в некотором минимуме, который может оказаться лишь локальным минимумом, а если повезет, то и глобальным.

После многократного предъявления примеров веса сети стабилизируются, причем сеть дает правильные ответы на все (или почти все) примеры из базы данных. В таком случае говорят, что «сеть обучена». В программных реализациях можно видеть, что в процессе обучения функция ошибки (например, сумма квадратов ошибок по всем выходам) постепенно уменьшается. Когда функ­ция ошибки достигает нуля или приемлемого малого уровня, тре­нировку останавливают, а полученную сеть считают натрениро­ванной и готовой к применению на новых данных.

Важно отметить, что вся информация, которую сеть имеет о задаче, содержится в наборе примеров. Поэтому качество обуче­ния сети напрямую зависит от количества примеров в обучающей выборке, а также от того, насколько полно эти примеры описы­вают данную задачу.

Для решения задачи обучения могут быть использованы следующие (итерационные) алгоритмы:

• 1. алгоритмы локальной оптимизации с вычислением частных производных первого порядка;
• 1. алгоритмы локальной оптимизации с вычислением частных производных первого и второго порядка;
• 2. стохастические алгоритмы оптимизации;
• 3. алгоритмы глобальной оптимизации.

К первой группе относятся: градиентный алгоритм (метод ско­рейшего спуска); методы с одномерной и двумерной оптимизацией целевой функции в направлении антиградиента; метод сопряженных градиентов; методы, учитывающие направление антигради­ента на нескольких шагах алгоритма [119, 122].

Ко второй группе относятся: метод Ньютона, методы оптими­зации с разреженными матрицами Гессе, квазиньютоновские ме­тоды, метод Гаусса-Ньютона, метод Левенберга-Марквардта [128, 131] и другие.

Стохастическими методами являются: поиск в случайном на­правлении, имитация отжига, метод Монте-Карло (численный ме­тод статистических испытаний).

Задачи глобальной оптимизации решаются с помощью пере­бора значений переменных, от которых зависит целевая функция (функция ошибки).

При использовании алгоритма обратного распространения ошибки сеть рассчитывает возникающую в выходном слое ошибку и вычисляет вектор градиента как функцию весов. Этот вектор указывает направление кратчайшего спуска по поверхности для данной точки, поэтому если продвинуться в этом направлении, то ошибка уменьшится. Последовательность таких шагов в конце концов приведет к минимуму того или иного типа. Определенную трудность здесь вызывает выбор величины шага.

При большой длине шага сходимость будет более быстрой, но имеется опасность пе­репрыгнуть через решение или уйти в неправильном направлении. Напротив, при малом шаге, вероятно, будет выбрано верное на­правление, однако при этом потребуется очень много итераций. На практике величина шага выбирается пропорциональной крутизне склона (градиенту функции ошибок). Такой коэффициент пропорциональности называется параметром скорости настройки. Пра­вильный выбор параметра скорости настройки зависит от конкретной задачи и обычно осуществляется опытным путем. Этот параметр может также зависеть от времени, умень­шаясь по мере выполнения алгоритма.

Алгоритм действует итеративно, и его шаги принято называть эпохами или циклами. На каждом цикле на вход сети последовательно подаются все обучающие наблюдения, выходные значения сравниваются с целевыми значениями, и вычисляется функция ошиб­ки. Значения функции ошибки, а также ее градиента используются для корректировки весов и смещений, после чего все действия повторяются. Начальные значения весов и смещений сети выбираются случайным образом, и процесс обучения прекращается либо когда реализовано определенное количество циклов, либо когда ошибка достигнет неко­торого малого значения или перестанет уменьшаться.

Другой подход к процедуре обучения сети можно сформулировать, если рассматри­вать ее как процедуру, обратную моделированию. В этом случае требуется подобрать та­кие значения весов, которые обеспечивали бы нужное соответствие между входами и желаемыми значениями на выходе. Такая процедура обучения носит название процедуры адаптации и достаточно широко применяется для настройки параметров ней­ронных сетей.

Каждый слой производственного сегмента решает свою функциональную задачу в рамках нейронной системы всего рынка. По этой причине процедуру обучения можно выполнять независимо для каждого слоя.

Процесс обучения требует набора примеров ее желаемого поведения - входов H и целевых выходов Ψ^оpt. Во время этого процесса веса настраиваются так, чтобы минимизировать некоторый функционал ошибки. По умолчанию, в качестве такого функционала для сетей с прямой передачей сигналов принимается среднеквадратичная ошибка между векторами выхода Ψ^оpt и Ψ.

При обучении сети рассчитывается некоторый функционал, характеризующий качество обучения:

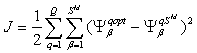,                                           (2.14)

где J - функционал; Q - объем выборки; М - число слоев сети; q - номер выборки; S^м - число нейронов выходного слоя; Ψ^q - вектор сигнала на выходе сети; Ψ^{q opt} - вектор желаемых (целевых) значений сигнала на выходе сети для выборки с номером q.

В случае использования линейной активационной функции нейронные сети первого слоя однослойные. В этом случае М = 1 и выражение для функционала принимает вид:

,                       (2.15)

где  - функция активации;  - сигнал на входе функции активации для  j-го нейрона; - вектор входного сигнала; w - число элементов вектора входа;  m - число нейронов в слое;  - весовые коэффициенты сети.

Включим вектор смещения в состав матрицы весов , а век­тор входа дополним элементом, равным 1.

Применяя правило дифференцирования сложной функции, вычислим градиент функционала ошибки, зная при этом, что функция активации дифференцируема:

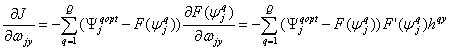.                      (2.16)

Введем обозначение:

.                              (2.17)

и преобразуем выражение (2.16) следующим образом:

.                     (2.18)

Полученные выражения упрощаются, если сеть линейна. Поскольку для такой сети выполняется соотношение , то справедливо условие . В этом случае выражение (2.16) принимает вид:

                                               .                                          (2.19)

Выражение (2.19) положено в основу алгоритма WH, применяемого для обучения ли­нейных нейронных сетей [132].

Линейные сети могут быть обучены и без использования итерационных методов, а путем решения следующей системы линейных уравнений:

.                     (2.20)

Если число неизвестных системы (2.20) равно числу уравнений, то такая система мо­жет быть решена, например, методом исключения Гаусса с выбором главного элемента. Если же число уравнений превышает число неизвестных, то решение ищется с использо­ванием метода наименьших квадратов.

В случае нелинейной функции активации для обучения нейронных сетей предлагается применить метод обратного распространения ошибки.

Алгоритм обратного распространения ошибки является одним из эффек­тивных обучающих алгоритмов [130]. По существу он представляет собой минимизационный метод градиентного спуска. Рассмотрим алгоритм обратного рас­пространения ошибки для нейронной сети с одним скрытым слоем. Предположим, что имеется A исходных примеров:

          = ,             (2.21)

где  - вектор желаемых выходов сети, соответствующий входному вектору .

Инициализируем вектор весов Ω случайным образом.

Теперь нужно осуществ­ить настройку весов сети с помощью процесса обучения. Для a-го примера выходы скрытых нейронов будут определяться выражениями:

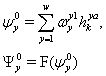,                                (2.22)

а выходы всей нейросети - выражениями:

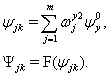                                                                                           (2.23)

В выражениях (2.22) и (2.23), F() - функция активации, например, сигмоидная функция.

Функционал квадратичной ошибки сети для данного входного образа имеет вид:

                                           (2.24)

Данный функционал подлежит минимизации. Классический градиентный метод оптимизации состоит в итерационном уточнении аргумента согласно формуле:

            ,                       (2.25)

где h - коэффициент скорости обучения 0<η<1.

Параметр η имеет смысл темпа обучения и выбирается достаточно малым для сходимости метода.

Функция ошибки в явном виде не содержит зависимости от веса , поэтому воспользуемся формулами неявного дифференцирования сложной функции:

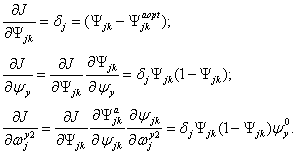                    (2.26)

Производная сигмоидной функции выражается только через само значение функции. Таким образом, все необходимые величины для подстройки весов выходного слоя получены.

Выполняется подстройка весов скрытого слоя:

                          (2.27)

Вычисляются производные функции ошибки:

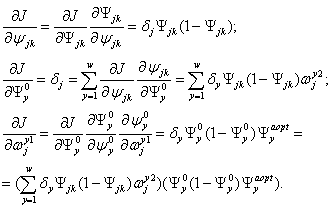           (2.26)

При вычислении d здесь и был применен принцип обратного распространения ошибки: частные производные берутся только по переменным последующего слоя. По полученным формулам модифицируются веса нейронов скрытого слоя.

Вычисления (2.22)-(2.26) повторяются для всех обучающих векторов. Обучение завершается по достижении малой полной ошибки или максимально допустимого числа итераций.

Сходимость метода обратного распространения весьма медленная. Невысокий темп сходимости является особенностью всех градиентных методов, так как локальное направление градиента отнюдь не совпадает с направлением к минимуму. Подстройка весов выполняется независимо для каждой пары образов обучающей выборки. При этом улучшение функционирования на некоторой заданной паре может приводить к ухудшению работы на предыдущих образах.

Несмотря на то, что алгоритм обратного распространения ошибки доста­точно прост, он требует обычно тысячи итераций для обучения нейросети. Если требований к точности нет, то следует использовать первый способ (2.14)-(2.20).

Для определения весов входов нейронов второго слоя, а также третьего слоя производственного сегмента нейронной системы обучение не требуется. Значения весов, в силу равнозначности положения всех производителей на рынке, выбираются равными. Никто из них не занимает по условию совершенной конкуренции привилегированного положения. Эти же принципы применимы и к товарам.

По аналогии определяются веса нейронной подсистемы потребительского сегмента рынка.

Главным этапом применения предложенной нейронной системы является процесс ее непосредственной эксплуатации. Цель этого этапа заключается в решении основной задачи - определении характеристик товара, обеспечивающих его производителю конкурентные преимущества и удовлетворяющего запросы потребителей.