
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.4. Результаты расчёта
Для того чтобы убедиться, что число k имеет силу закона, построим график зависимости больших полуосей орбит всех планет и Плутона табл. 2 от числа k и проведём по этим точкам регрессионную зависимость, проходящую через начало координат, учитывая центральное действие сил гравитации (рис. 3).

Рис. 3. Зависимость большой полуоси орбиты планеты (точки) от числа k. Регрессия (прямая) проведена через начало координат
При проведении регрессионной зависимости получены следующие статистические данные: коэффициент детерминации R2 = 99,957 %, критерий Фишера F = 32141, критерий Стьюдента t = 179,3. На основании такой статистики можно утверждать, что полученная регрессия имеет силу закона. Длина волны основного гравитона Солнца равна ?o = 735,9(9,5) млн. км (в скобках приведено стандартное отклонение) или ?o = 7,359(0,095*1011) м.
Можно воспользоваться еще одним способом расчета ?o. Для этого значение большой полуоси орбиты каждой планеты делится на соответствующее значение k (столбец 4 табл. 2). Полученные результаты (без учета планеты Плутон [7]) обрабатываются программой Excel Анализ данных / Описательная статистика. В этом случае результат равен ?o = 737,55(30,27) млн. км и согласуется с предыдущим в пределах ошибки.
Если масса Солнца равна Mo = 1,99*1030 кг, то значение «магнитной» гравитационной константы получим:
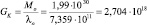 кг/м.
кг/м.
Другое значение равно
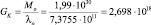 кг/м.
кг/м.
Для вычисления скорости гравитона используем те же процедуры, что и для вычисления периода волны основного гравитона Солнца. По данным табл. 2 построим зависимость средней скорости движения планеты по орбите V (столбец 6 табл. 2) от величины 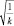 и проведем по этим точкам регрессионную зависимость, проходящую через начало координат (рис. 4).
и проведем по этим точкам регрессионную зависимость, проходящую через начало координат (рис. 4).

Рис. 4. Зависимость средней скорости движения планеты по орбите V
от величины 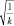 – точки. Прямая линия – уравнение регрессии по точкам
– точки. Прямая линия – уравнение регрессии по точкам
Регрессионная зависимость имеет силу закона и показала следующий результат Vg = 13,336(0,185) км/с = 1,3336(0,0185)*104 м/с при статистических показателях: коэффициент детерминации R2 = 99,976 %, критерий Фишера F = 28987, критерий Стьюдента t = 170,3.
Учитывая соотношение 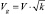 , вычислим соответствующие скорости для каждой из планет (столбец 7 табл. 2) и, обработав эти данные программой Excel / Анализ данных / Описательная статистика, получим результат:
, вычислим соответствующие скорости для каждой из планет (столбец 7 табл. 2) и, обработав эти данные программой Excel / Анализ данных / Описательная статистика, получим результат:
Vg = 13,413(0,275) км/с = 1,3413(0,0275)*104 м/с,
который согласуется в пределах ошибки с предыдущим значением.
Теперь имеется возможность вычислить значение гравитационной константы GN по двум вариантам вычислений и сравнить с существующим значением GN = 6,6726*10–11 м3/(кг*с2):
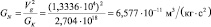
и
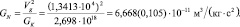
Второй вариант лучше согласуется с известным GN тем более, что такой вариант статистической обработки верен. Статистическая обработка с помощью регрессии использована для того, чтобы показать функциональную значимость приведенных соотношений.
Расчёта показал следующие значения новых констант [8]:
- длина волны основного гравитона Солнца ?o = 7,3755(0,3027)*1011 м;
- период основного гравитона Солнца 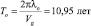 ;
;
- «магнитная» гравитационная константа GK =2,698*1018 кг/м;
- скорость гравитона Vg = 1,3413(0,0275)*104 м/с;
- константа структуры 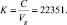
В заключение параграфа следует вспомнить, что для расчета новых констант использовались соотношения квантовой механики, несколько модифицированные для гравитационной системы, и законы оптики. В процессе вычисления констант получены статистически значимые зависимости, обладающие силой закона. С точки зрения физического смысла получен важный результат – пространство является носителем гравитационного поля, однозначно связано с массой и обладает волновыми свойствами [9].
Через коэффициент структуры k показана основная структура волнового пространства вокруг Солнца и вычислен целый ряд фундаментальных констант и констант, необходимых для описания Солнечной системы.
