Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

СТАТИСТИЧЕСКИЕ МОДЕЛИ В КВАНТОВОЙ ФИЗИКЕ ЭКОЛОГИИ И ЭКОНОМИКЕ

Рау В. Г., Рау Т. Ф., Малеев А. В.,

§ 1.2. Соотношение неопределенностей Гейзенберга

Таким образом, в предыдущем параграфе показано, что «материализовать» Ψ-волны де-Бройля не удалось ни в виде самостоятельного поля, ни в виде частиц. Для выяснения физического смысла волн де-Бройля необходимо вновь вернуться к эксперименту по дифракции электронов и провести его анализ.

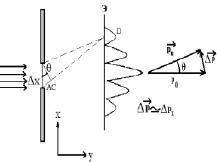
Рис. 2. К выводу соотношения неопределенностей

Будем считать, что нам удалось подобрать такую «щель», проходя через которую поток электронов, пущенных как поодиночке, так и в пучке, образует на экране картину дифракции.

Замена реальной кристаллической решетки на обыкновенную щель (для простоты рассуждений) не изменяет сущности процесса. Принципиально, эксперимент с одной щелью сохраняет все основные особенности реальной экспериментальной установки.

На рис. 2 изображены: щель, размеры которой равны Δx, угол рассеяния электронов θ, характеризующий «n»-й порядок дифракции, экран, на котором фиксируется картина рассеяния и график интенсивности (почернений) на экране.

Если щель Δx относительно λ велика, то дифракционная картина «сжата» и тогда . Приближенная оценка позволит связать размеры щели с наблюдаемыми размерами дифракционной картины:

а) AC = nλD (условие максимума);

б) ;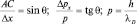

в)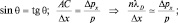

г)

Полученный результат дает возможность качественно провести анализ дифракции. Более точные количественные оценки экспериментов, а затем и последующие вычисления в рамках теории квантовой механики, позволили записать окончательно соотношение, впервые полученное Гейзенбергом:

ΔxΔpx ≥ ħ (соотношение Гейзенберга). (1.2.1)

В рассмотренном эксперименте Δx – набор возможных значений x – координат объекта, а Δpx – набор возможных значений проекции импульса. Более точно измерить одновременно значение x и px невозможно, поэтому величины Δx и Δpx характеризуют неопределенности в значениях координат и импульсов микрообъекта, измеренных в момент прохождения его через щель. Если пытаться уменьшать неопределенность Δx (сужать размеры щели), то возрастает Δpx, дифракционная картина становится значительно более широкой, то есть, «размывается» (этот же вывод следует и из экспериментов по дифракции света на щели).

Вывод: произведение неопределенностей в значении координат и соответствующих проекций импульсов микрообъекта, измеренных в один и тот же момент времени, не меньше ħ, где .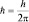

Итак, представления о том, что каждому движению частицы сопутствует некоторый волновой процесс с волновой Ψ-функцией и входящей в нее волной де-Бройля, привели к соотношению неопределенностей, запрещающему точное одновременное измерение координат и соответствующих проекций импульса. Это, с точки зрения классической механики, запрещает и точную фиксацию состояния микрообъекта, так как она, как мы это знаем из законов классической механики, определяется координатами и импульсами частиц. Более того, с точным заданием начальных значений координат и импульсов при решении уравнений движения частиц, мы связываем причинно-следственные отношения.

Возникают дополнительные трудности и философского характера. Нет ли в микромире нарушений причинно-следственных связей? Познаваем ли микромир? Возможны два принципиально разных ответа на эти вопросы. Первый ответ действительно признает непознаваемость микромира вследствие невозможности точного определения состояния движения. Второй ответ может быть основан на признании того факта, что состояние микрообъекта определяется не так, как у макрообъекта. Невозможность точного измерения координат и импульсов означает, что эти переменные исключают друг друга, они «не существуют» одновременно. К последнему можно лишь добавить, что уменьшение размеров объектов (и их масс соответственно) привело к появлению новых волновых свойств. Поэтому состояние должно быть описано с помощью волновой функции, которая для движения свободной частицы совпадает с «плоской монохроматической волной»:

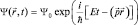. (1.2.2)

Будем придерживаться второй, более позитивной оценки действия закона соотношений неопределенностей (1.2.1). В этом случае для характеристики состояния объекта необходимо разобраться в используемых нами терминах. Новым является понятие неопределенности. В каких единицах ее измерить? Как математически связать неопределенности с волновой функцией?

Из соотношения неопределенностей следует, что неопределенность координаты связана с набором возможных ее значений от 0 до Δx и заранее не определено лишь то, какое из этих значений «появится» у пролетающего электрона. Эта ситуация похожа на неопределенности исхода при бросании игральной кости («кубика») случайным образом. В последнем примере «мерой неопределенности» исхода являлась вероятность появления случайной величины (цифры на грани кубика). Если применить ту же схему к движению электрона и считать координаты и импульсы случайными непрерывными величинами, то вместо вероятности необходимо ввести функцию плотности вероятности 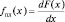, где dF характеризует вероятность обнаружения у микрообъекта случайной координаты x в интервале dx (от x до x + dx).

Таким образом, приходим к математическому описанию движения микрочастиц на основе аппарата теории вероятностей. Остается только связать комплексную волновую функцию состояния объекта с вещественной функцией плотности вероятности. Как известно, в эксперименте, связанном с фиксацией волны, у нее обычно измеряется квадрат ее модуля (вспомним, что для волны напряженности электрического поля фиксируется плотность энергии .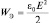

Подобные соображения позволили М. Борну и В. Гейзенбергу предположить, что функция плотности вероятности совпадает с квадратом модуля волновой функции 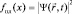. В этом случае, измеряемые величины вероятностей являются вещественными.

Таким образом, волновые свойства микрообъектов можно считать вероятностными свойствами, волны де-Бройля можно назвать «волнами вероятности», а смысл волновой Ψ-функции заключается в том, что квадрат ее модуля является функцией плотности вероятности обнаружения микрообъекта в определенном состоянии.

Выводы:

1) микрообъекты обладают волновыми свойствами, подтвержденными опытами по дифракции электронов;

2) состояние микрообъектов определяется волновой функцией, квадрат модуля которой характеризует функцию плотности вероятности обнаружения микрообъекта в определенном состоянии;

3) соотношения неопределенностей Гейзенберга представляет собой новый экспериментальный физический закон, фиксирующий наличие у микрообъектов волновых вероятностных свойств.

Подтверждением правильности открытия нового закона явился факт существования «естественной ширины спектральной линии». Действительно, физиками-спектроскопистами было замечено, что существуют ограничения на точность определения длин волн в спектре излучения вещества, как призматическими спектрографами, так и дифракционными. Простое решение нашлось при использовании соотношения Гейзенберга. Формально, по «размерности», заменяя переменные в соотношении неопределенностей x = ct и 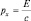(для фотонов), имеем: 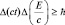, получим ΔEΔt ≥ ħ.

Оказывается, что чем дольше существует система в состоянии с энергией En, т.е. чем стабильнее состояние, тем меньше «разброс» или «неопределенность» в значении энергии. И наоборот, например, в атоме водорода стационарные состояния с n ≥ 2 являются нестабильными, неустойчивыми, длящимися в течение τ = Δt = 10–8 c (время «возбужденного состояния» оценено «классически»).

Тогда минимальный «разброс» в значении энергии будет определяться из соотношения (ΔE)minΔt = ħ. При Δt = τ, 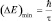, что позволяет перейти к соответствующей «поправке» для каждой длины волны: 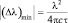. Эта величина (Δλ)min называется «естественной шириной спектральной линии» (рис. 3).

4. Состояния в системе микрообъектов (атомной системе) квантованы, то есть переменные состояния принимают дискретный ряд значений, что подтверждается опытами Франка и Герца, а также наличием линейчатой структуры спектра излучения атомов. Используем полученную информацию для решения задачи.

Задача. Оценить время «жизни» волнового пакета в вакууме, используя соотношение неопределенностей.

Решение. Ограничимся для простоты нерелятивистским приближением: p << m0c, m0 – масса покоя частицы. Тогда, в отсутствии внешнего взаимодействия, полная энергия частицы совпадает с кинетической, и 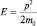, откуда следует: 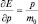. Для оценки времени расплывания волнового пакета получаем (согласно соотношению неопределённостей):

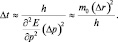
В случае макроскопической частицы, имеющей массу, например 1 грамм, и размер Δr = 0,1 см, время расплывания окажется, то есть такой волновой пакет фактически не будет расплываться. В случае же микрочастицы вроде электрона, чья масса порядка 10–30 кг, Δr = 10–13 см, волновой пакет расплывется почти мгновенно: Δt ~ 10–26 с. Из-за того, что волновой пакет микрочастицы в общем случае расплывается весьма быстро, для их (частиц) успешного описания следует составлять волновой пакет из волн, разброс значений волновых чисел которых невелик, то есть Δk << k0.

Для фотона, энергия которого, выраженная через импульс равна Eγ = pc и групповая, и фазовая скорости в вакууме совпадают и равны с.