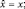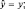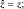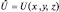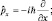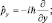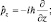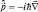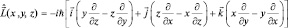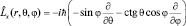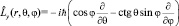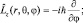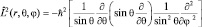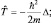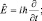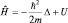Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 1.4. Операторы квантовой механики. Уравнение Шредингера
В тексте § 1.3 мы выяснили, что каждой измеряемой физической величине («наблюдаемой» – как ее часто называют) следует поставить в соответствие некоторый оператор. Вид оператора, как и определение величины (например, скорости: 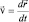 ) не зависит от выбора ситуации, в которой найден оператор, поэтому оператор можно получить и в каком-либо конкретном случае, например, при свободном движении микрообъекта. Тогда решением уравнения должна быть функция состояния как собственная функция оператора квантовомеханической величины.
) не зависит от выбора ситуации, в которой найден оператор, поэтому оператор можно получить и в каком-либо конкретном случае, например, при свободном движении микрообъекта. Тогда решением уравнения должна быть функция состояния как собственная функция оператора квантовомеханической величины.
Чтобы сохранить соответствие между квантовой механикой и классической механикой, будем присваивать оператору «имя» механической величины, тогда появятся операторы координаты, импульса, момента импульса, энергии и т.д., но все они удовлетворяют условию линейности оператора:
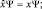


 (1.4.1)
(1.4.1)
Как легко видеть, операция умножения на соответствующую величину всегда удовлетворяет записанным равенствам, но важно, чтобы эти величины не были независимы: ведь в классической механике энергию системы, например, всегда можно выразить через координаты и импульсы. Поэтому за простейший оператор «умножения на величину» выберем оператор координаты объекта. Тогда одно уравнение:  означает простое тождество: xΨ = xΨ и оператор потенциальной энергии
означает простое тождество: xΨ = xΨ и оператор потенциальной энергии  также оказывается фиксированным. (Например, если xΨ = xΨ, то mgxΨ = mgxΨ, но справа mgxΨ = U(x)Ψ, а значит и слева
также оказывается фиксированным. (Например, если xΨ = xΨ, то mgxΨ = mgxΨ, но справа mgxΨ = U(x)Ψ, а значит и слева 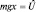 , так как справедливо равенство
, так как справедливо равенство  ). Такой подход к операторам носит название «координатного представления». Теперь вычислим оператор проекции импульса при условии, что известна волновая функция, как функция состояния:
). Такой подход к операторам носит название «координатного представления». Теперь вычислим оператор проекции импульса при условии, что известна волновая функция, как функция состояния:

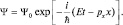
Слева стоит величина px как собственное значение искомого оператора 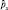 .
.
Для «появления» px перед функцией Ψ, необходимо продифференцировать ее по переменной «x»:
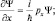
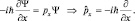
Аналогично находим оператор энергии  дифференцированием Ψ-функции по «t»:
дифференцированием Ψ-функции по «t»:
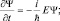
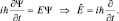
Теперь вычисляем оператор кинетической энергии:
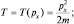
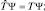
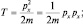
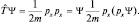
Полагая pxΨ = Φ, имеем:
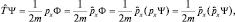
а тогда 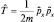 . Двойное применение одного и того же оператора будем обозначать как квадрат оператора, после чего делаем вывод:
. Двойное применение одного и того же оператора будем обозначать как квадрат оператора, после чего делаем вывод:
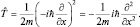
В трехмерном случае
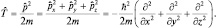
Сравнивая выражения: 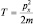 и
и 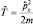 можно считать такое совпадение форм записи способом перехода от классических величин к квантовым: соотношения (действия) между операторами в квантовой механике аналогичны соотношениям между величинами в классической механике.
можно считать такое совпадение форм записи способом перехода от классических величин к квантовым: соотношения (действия) между операторами в квантовой механике аналогичны соотношениям между величинами в классической механике.
Формально, всякую величину классической механики, выраженную через координаты и импульсы, можно переписать, «приделав» всем величинам «шляпы» и тем самым определить оператор данной величины. Например, для вычисления оператора кинетической энергии 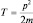 будем иметь:
будем иметь:
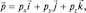
тогда 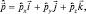 а
а
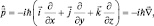
то есть 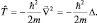
Вычислим оператор момента импульса 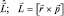 . В декартовой системе координат
. В декартовой системе координат 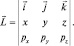 Тогда, следуя найденному соответствию, имеем:
Тогда, следуя найденному соответствию, имеем:
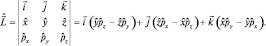 (1.4.2)
(1.4.2)
В частности, для проекции Lx получим:
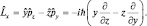
Оператор энергии частиц, находящихся в стационарном состоянии, ищем через операторы кинетической и потенциальной энергии тем же способом, что и выше.
H = T + U,
а тогда
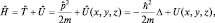
где Δ – оператор Лапласа (в декартовой системе координат равный сумме вторых производных):
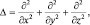
тогда  ,
, 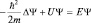 или
или 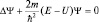 . Полученное уравнение
. Полученное уравнение  в форме:
в форме:
(I) 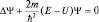
является уравнением движения микрообъекта и называется стационарным уравнением Шредингера, по фамилии австрийского физика Э. Шредингера, впервые его получившего из уравнения волны.
Уравнение
 или
или 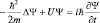 (1.4.3)
(1.4.3)
названо нестационарным уравнением Шредингера. Для того, чтобы в (I)-м, стационарном уравнении Шредингера, избавиться от времени, представим 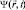 в виде произведения:
в виде произведения: 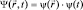 или в вероятности трактовке
или в вероятности трактовке 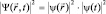 как умножение плотностей вероятности независимых событий (
как умножение плотностей вероятности независимых событий ( и t – независимые переменные). Подставляя
и t – независимые переменные). Подставляя 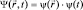 в уравнение (I), имеем:
в уравнение (I), имеем:
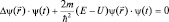 ,
,
а так как операция Δ связана лишь с дифференцированием по координатам, то ψ(t) можно вывести за знак операции, после чего окончательно получим:
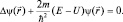 (1.4.4)
(1.4.4)
Используя преобразования координат при переходе от декартовой системы к сферической, имеем для операторов 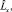
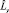 и
и 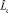 выражения:
выражения:
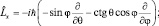
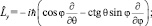
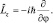
И, наконец, опуская подробности, для 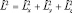 будем иметь:
будем иметь:
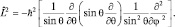
Сведем в одну табл. 2 все необходимые для наших расчетов операторы и уравнения движения квантовой механики.
Таблица 2
Список операторов квантовой механики
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В качестве примера, проверим некоторые операторы на коммутативность и самосопряженность.
1. Пусть заданы  и
и 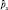 . Коммутатор
. Коммутатор 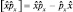 . Применим оператор
. Применим оператор 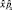 к функции Ψ:
к функции Ψ:
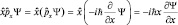 .
.
Аналогично действуя на Ψ оператором 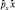 , имеем:
, имеем:
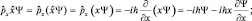
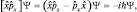
т.е. 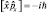 .
.
Операторы  и
и 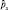 некоммутируют, а, следовательно, нельзя одновременно измерить соответствующие им физические величины. Легко видеть, что
некоммутируют, а, следовательно, нельзя одновременно измерить соответствующие им физические величины. Легко видеть, что 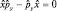 , т.е.
, т.е. 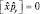 и соответствующие величины поддаются одновременному измерению. Как и следовало ожидать, математический аппарат оперативного исчисления правильно отражает экспериментальные факты (соотношение неопределенностей).
и соответствующие величины поддаются одновременному измерению. Как и следовало ожидать, математический аппарат оперативного исчисления правильно отражает экспериментальные факты (соотношение неопределенностей).
2. Проверим самосопряженность оператора 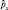 .
.
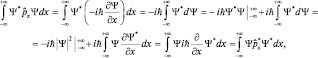
что и доказывает самосопряженность оператора проекции импульса. На этих примерах закончим первичное знакомство с математическим аппаратом квантовой механики.