Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 1.7. Квантовомеханические модели. Квантовый осциллятор
Будем называть осциллятором такую систему, которая движется под действием сил, пропорциональных смещению, или в поле квазиупругих потенциальных сил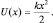 
Если иметь дело с классическим осциллятором, то наблюдая (фотографируя) его в «случайные» моменты времени, можно вычислить функцию плотности вероятности его обнаружения в точке x в виде:
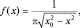(1.7.1)
где x0 – амплитудное отклонение. Эта функцию называют функцией Коши. Очевидно, что осциллятор чаще можно «встретить» вблизи амплитудного значения координаты, чем в центре. Теперь определим характер стационарного движения квантовомеханического осциллятора (КМО). Запишем уравнение движения:
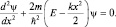
Обозначим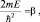 
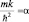и произведем замену переменной в виде: 
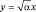. Тогда
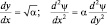
и уравнение Шредингера примет вид:
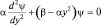или 
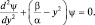(1.7.2)
Дифференциальные уравнения такого вида хорошо изучены в математике. Да и физически поддаются простому анализу. Сравните: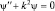 
(имеющее экспоненциальную функцию в качестве решения) и 
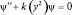. Поэтому можно искать общее решение данного уравнения в виде:
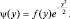
Дифференцируя ψ(y) дважды, имеем:
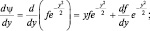
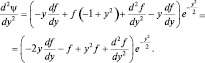
Подстановка полученного выражения в уравнение (1.7.2) дает:
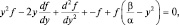
т.е.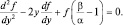 
(1.7.3)
Осталось найти вид функции f(y). Так как любую функцию можно представить степенным рядом, то следует искать решение уравнения в виде ряда:
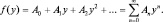
Тогда имеем: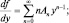 
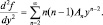
Если ввести k = n – 2, то n = k + 2 и суммирование начнется с k = 0. Тогда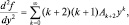 
но так как k – это просто индекс суммирования, то можно его обозначить по-прежнему, т.е.
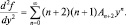
Уравнение (1.7.3) примет вид:
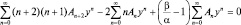
или
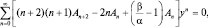
что возможно только тогда, когда выражение в квадратных скобках обращается в нуль при любом индексе суммирования. Тогда имеем:
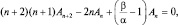
откуда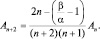 
(1.7.4)
Полученная рекуррентная формула связывает все коэффициенты ряда. Достаточно задать A0 и A1, как функция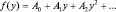 
будет определена и решение ψ(y) оказывается найденным. Но при y → ∞, f(y) → ∞ быстрее, чем 
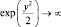. Физическое требование конечности (ψ(y) → 0, где y → ∞) можно выполнить при ограниченном числе членов в степенном ряду. Тогда fn(y) → ∞ медленнее, чем 
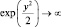. Обрывая ряд на первом члене, получим первое решение, на втором – второе и т.д. «Технически» это удается сделать, если An ≠ 0, а An+2 = 0, как при n – четном, так и нечетном. Полученный полином и является частью искомого решения. Тогда 
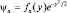. Из соотношения (2.4.7) при An+2 = 0, а An ≠ 0 имеем: 
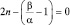, откуда следует, что 
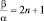. Рекуррентная формула (1.7.4) позволяет вычислить и коэффициенты ряда с меньшими индексами. Действительно, коэффициенты An и An–2 связаны следующим образом:
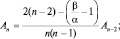
в соответствии с (1.7.4), но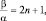 
а тогда 
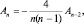откуда 
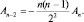Аналогично,
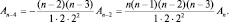
Если положить An = 2n, получим полиномы, именуемые полиномами Эрмита: H0 = 1, H1 = 2y, H2 = 4y2 – 2 и т.д.
Наконец, необходимо, чтобы выполнялось при каждом Hn условие нормировки волновой функции. Положим, например, fn = CnHn, где Cn – нормирующий множитель, а тогда для состояния n = 0,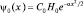 
имеем:
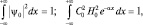
но H0 = 1, откуда следует: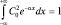 
или после вычислени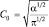й: 
и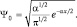 
Аналогично рассуждая, имеем для любого n-го состояния: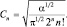 
Вид функции плотности вероятности аналитически и графически представлен на рис. 11 (а, б). При n → ∞ ход «классической» кривой функции плотности вероятности соответствует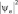 
, как это и должно быть при предельном переходе от квантовых представлений к классическим (принцип соответствия).
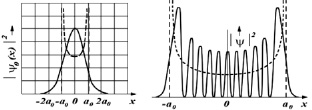
а б
Рис. 11. Плотность вероятности нахождения КМО в различных состояниях
Вычислим энергию осциллятора в n-м состоянии. В рекуррентной формуле:
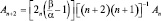
коэффициент An+2 должен обращаться в ноль, поэтому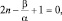 
но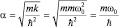 
. После преобразований
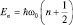(1.7.5)
или, в частном, но очень важном случае,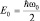 
. Для энергии переходов между двумя соседними уровнями имеем: 
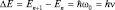, что соответствует гипотезе Планка о квантовании энергии в спектре излучения черного тела: в стенках черного тела расположены атомные (квантовые) осцил- ляторы (см. рис. 12).
Выводы:
1. Состояния и энергия квантового осциллятора квантованы.
2. Вероятность обнаружения осциллятора за пределами амплитудного значения не равна нулю.
3. При больших квантовых числах поведение квантового осциллятора аналогично поведению классического.
4. Минимальная энергия осциллятора не может быть равной нулю.
Реальный квантовый осциллятора существует, например, в твердом теле (в стенках полости черного тела). Это либо молекулярные диполи, либо ионы в узлах кристаллической решетки. Молекулярные диполи обмениваются друг с другом фотонами εγ = hv, а ионы «передают» вдоль «узлового» ряда решетки «звуковые» кванты – фононы с энергией Eф = ħω. В первом случае обменное взаимодействие осуществляется реальными частицами электромагнитного поля, а во втором – «квазичастицами», которые самостоятельно, без среды существовать не могут. Во многих процессах поведение фононов и фотонов идентично.