Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 1.10. Периодическая система химических элементов. Принцип Паули
После открытия спина следует определить состояние электрона не тремя, а четырьмя квантовыми числами: n, l, ml, ms включив в этот перечень и магнитное спиновое квантовое число.
И еще один экспериментальный факт необходимо каким-то образом ввести в основу построения квантовой механики. Опыт показывает, что объем, принадлежащий атому вещества тем больше, чем больше его порядковый номер (то есть, заряд ядра и количество электронов). Следовательно, электроны не могут все вместе находиться в одном и том же, даже самом устойчивом состоянии близко к ядру и они распределяются по состояниям. Правило, запрещающее двум (и более) электронам находиться в одном и том же состоянии атома, было открыто Паули и называется «принципом запрета Паули»: в атомной системе нельзя обнаружить двух или несколько электронов в одном и том же квантовом состоянии.
Принцип Паули полностью не отвергает законов устойчивости системы, сформулированных еще в механике, и известных как принцип минимума потенциальной анергии, а лишь ограничивает их применение. С точки зрения расчета энергии атома минимальное ее значения соответствуют минимальным величинам квантовых чисел n и l. Поэтому распределение электронов по состояниям следует начинать. Так, на примере атома натрия будем иметь: Элемент Na, порядковый номер Z = 11, число электронов Z = 11.
Электронная «формула» атома Na может быть записана как 1s22s22p63s1, где верхняя цифра показывает количество электронов в данном состоянии. Часто (рис. 19) в химии можно встретить и такое представление распределения электронов по ячейкам.
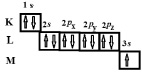
Рис. 19. Распределение электронов по ячейкам – состояниям
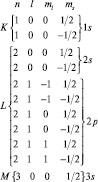
На К-слое Na, располагаются 2 электрона, на L-слое 8 электронов, на М-слое 1 электрон. (Легко доказать, что на слое с главным квантовым числом n может находиться не более 2n2 электронов). У атома Li c порядковым номером Z = 3 в таблице Менделеева электроны располагаются следующим образом: 1s22s1. Легко видеть, что повторяемость свойств в системе элементов Менделеева связана с подобием «внешнего» строения атомов – именно внешние электроны наиболее легко вступают во взаимодействие с электронами других атомов, образуя химическую связь. Электроны, принадлежащие одной оболочке, располагаются на одном и том же среднем расстоянии от ядра, образуя электронные «слои».
Итак, электронная плотность в каждом состоянии с квантовый числом l называется «орбиталью»; так, например, при l = 0, s-орбиталь; при l = 1 px-, py-, pz-обритали и т.д. Орбитали отдельных электронов в атоме могут «объединяться с образованием атомных орбиталей (АО), что было показано ранее на примере молекулы водорода. Это возможно, если соответствующие электронные плотности «перекрываются». Аналогично, при перекрывании атомных орбиталей отдельных атомов может образоваться общая молекулярная орбиталь. Это обобществление электронов с образованием молекулярных орбиталей (МО) и приводит к так называемой ковалентной химической связи. Метод расчета молекулярных орбиталей называется МОЛКАО – молекулярная орбиталь (МО), как линейная комбинация (ЛК) атомных орбиталей (АО), что математически записывается так:
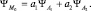
Так как ΨA-функции могут быть и вещественными, и комплексными, то их сложение может привести как к образованию химической (ковалентной) связи, так и к отсутствию таковой. Поэтому, например, два атома кислорода образуют устойчивую молекулу кислорода О2, а молекула Ne2 из двух атомов неона не образуется.
Рассмотрим строение вещества на основе ковалентных связей и понятие о зонной теории строения твердых тел.
Органические молекулы, образующие основу жизни на Земле, содержат в качестве «обязательного» элемента – атом углерода. Знание структур молекул этого класса веществ может прояснить многие проблемы химии, медицины, сельского хозяйстве, физиологии» ботаники и других наук.
Электронная формула углерода выглядит следующим образом: 1s22s22p2. При небольшом «возбуждении» электроны перестраиваются в состояние 1s22s12p3. По энергиям состояния 1 и 2 очень близки. Такая перегруппировка, тем не менее, резко изменяет «пространственные» характеристики электронной плотности атома. Возможны следующие варианты.
1. На L-слое электронные плотности четырех электронов (в s-состоянии и трех р-состояниях) образуют четыре sр3-атомные орбитали. Их равноправие приводит к тому, что в пространстве они образуют тетраэдрическое окружение ядра атома углерода «гибридными» sр3 – орбиталями (рис. 20а).
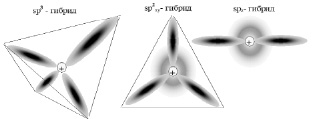
а б в
Рис. 20. Электронная плотность в атоме углерода
2. Возможно образование трех sp2 (из s-, px-, py-электронов) атомных орбиталей, располагающихся также равноправно относительно друг друга. Очевидно, три sp2-гибрида расположатся под углом α = 120° по отношению друг к другу. Тогда четвертый электрон займет оставшуюся рz-орбиталь, идущую в направлении перпендикулярном к плоскости треугольника из sp2-гибридов (рис. 20б).
3. Если осуществляется перекрывание электронных плотностей s- и рz-состояний, образуются две sp-орбитали (sр-гибридизация), а два других электрона останутся в своих «собственных» состояниях рx и рz. Поэтому угол между sp-гибридами составляет α = 180° (рис. 20в).
По такому же принципу образуются и молекулярные орбитали: обобществление электронов, обмен электронами между атомами и приводит к ковалентной связи, физики при этом говорят, что между атомами осуществляется «обменное» взаимодействие. На рис. 21 изображены молекула бензола C6H6, образование которой теперь понятно без обсуждения и структура комплексного иона соединения кобальта с 6-ю молекулами карбамида. Окончательное решение вопроса о связи атомов определяется расчетом линейных комбинаций атомных Ψ-функций с учетом их знаков. Если в результате «перекрывания» волновые функции компенсируют друг друга «по знаку», то электронная плотность может оказаться равной нулю и связь не образуется.
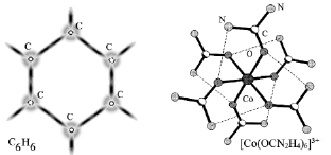
Рис. 21. Модель связей в молекулах органических и комплексных соединений
Теперь рассмотрим, что происходит с «энергетической структурой атомов при их объединении в молекулы и в твердые тела. При сближении атомов появляется воздействие электрического и магнитного поля одного атома на состояние движения «внешних» электронов в другом атоме. Это действие, конечно» носит характер взаимодействия. Образуется единая система, в которой по принципу Паули уже нельзя обнаружить двух электронов в одинаковых состояниях. Энергетические уровни атомов «расщепляются», образуются новые состояния, как комбинация исходных состояний, и при этом взаимодействующие электроны, принадлежащие одинаковым оболочкам, объединяются, образуя целую полосу иди «зону» близких по значению энергии уровней. Так (не в масштабе), для твердого тела, состоящего из атомов Na образуются зоны: на М-слое (n = 3) образуется зона, состоящая из двух частей; первая – заполнена электронами (заштрихована), а вторая часть не заполнена. Ниже лежащие слои заполнены электронами полностью.
Не следует понимать слово «заполнены», как появление электронов в определенном месте пространства. Речь идет об энергетической зоне, а это пространство абстрактно. Видно также, что переход из «заполненной зоны» в свободную не нуждается в большой энергии перехода. Достаточно приложить к концам натриевой проволоки электрическое поле с разностью потенциалов U, как начинается переход электронов в свободную зону, и вещество становится проводником электрического тока.
Другой результат получим, если в качестве образца примем кристалл алмаза. Энергетические зоны в алмазе не перекрываются (в состав алмаза входит углерод: 1s22s22p2), ближайшее «расстояние» между свободной и заполненной зонами на L-слое составляет величина ΔW = 6 эВ («энергетическая щель»). Энергии обычного электрического поля для перехода электронов в свободное «проводящее» состояние недостаточно» Но в кристаллическом кремнии (1s22s22p63s33p4), несмотря на такое же строение решетки, как у алмаза, эта щель составляет величину ΔW = 6 эВ. При низких температурах средней энергии электронов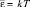 
недостаточно для участия в электрическом токе, но при высоких температурах этот материал ведет себя как проводник. Таким образом зонная теория твердых тел объясняет существование проводников, диэлектриков и полупроводников. На сопротивление (и проводимость) проводников влияют «примесные атомы».
Каким же образом электроны проходят через запрещенную зону? Каким образом они становятся свободными в твердом теле? Действительно, обычно «высота барьера» удерживающих кулоновских сил бывает значительнее, чем кинетическая энергия электронов. Аналогичные вопросы возникают при анализе явления α-распада радиоактивного ядра, где высота потенциального барьера также выше, чем энергия α-частицы. Ввиду важности этого вопроса рассмотрим его подробнее.