Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 2.1. Введение в статистическую физику. Термодинамические системы
Объектом исследования в статистической физике и термодинамике является термодинамическая система.
Определение. Термодинамической системой (ТС) будем называть такую физическую систему, которая состоит из большого числа частиц или характеризуется большим числом степеней свободы. Исторически сложились два основных подхода к исследованию термодинамических систем: первый, структурный, второй, системный или феноменологический. Эти подходы в настоящее время, привели к двум различным разделам физики. Первый называется «Статистическая физика» (иногда «Молекулярно-кинетическая теория», как частный случай), а второй – «Термодинамика». Основным понятием, характеризующим термодинамическую систему, является состояние.
Определение. Состоянием ТС будем называть минимальную совокупность параметров системы (переменных состояния), позволяющих прогнозировать ее поведение. Если известны переменные состояния в начале процесса, то, в принципе, возможно их знание в конце процесса, то есть, как в механике, «в начальный и конечный моменты времени». Тем не менее, квантовая механика внесла поправку в понимание переменных состояния: при статистическом подходе, из-за принципа неопределенности, параметры состояния удается прогнозировать лишь с определенной вероятностью. Поэтому функция состояния системы имеет вид функции распределения вероятностей.
В термодинамике, изменение состояния называют процессом, а в статистике, изменение состояния влияет на характеристики распределения, в частности, на средние значения переменных состояния. Поэтому в термодинамике, функция состояния не носит вероятностного характера и определяется однозначно через переменные состояния. Связь между переменными состояния, выраженная в виде зависимости одной переменной через другие называют в термодинамике уравнением состояния. Если в качестве термодинамической системы выбрать газ, состоящий из N– большого числа молекул, то все основные понятия можно представить в виде системной табл. 5.
Таблица 5
Два подхода к термодинамической системе
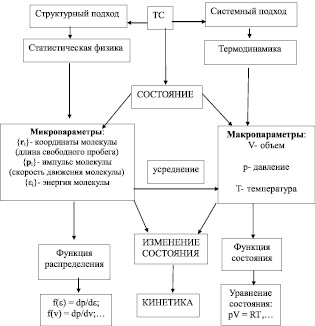
Рассмотрим фазовое пространство термодинамической системы. Если использовать механический подход к термодинамической системе, то каждую молекулу можно считать материальной точкой и определить ее состояние через две независимые переменные состояния: проекции координат каждой точки и проекции импульса каждой точки, заданных в пространстве координат и импульсов. Так, например, для механической системы – классического одномерного осциллятора (маятника) – пространство состояния двумерно и его стационарное движение моделируется эллипсом, так как полная энергия есть величина постоянная
(стационарность) и позволяет однозначно записать связь между координатой (определяющей потенциальную энергию) и импульсом (определяющим кинетическую энергию) осциллятора в виде:
,
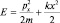откуда следует уравнение эллипса:
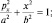
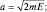
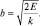
При наличии трения изменяется величина полной энергии маятника и новое стационарное состояние фиксируется в точках, принадлежащих эллипсам с меньшими величинами полуосей (рис. 25).
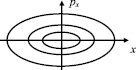
Рис. 25. Фазовые траектории классического линейного осциллятора
Кривые, изображенные на рис. 25, называют фазовыми траекториями системы, а само пространство состояний называют фазовым пространством. Видно, что фазовые траектории стационарных состояний непрерывны и не пересекаются. Глядя на совокупность точек любой из фазовых траекторий невозможно определить: имеем мы дело с одним маятником, находящемся в различных точках-состояниях в разные моменты времени, либо речь идет о различных маятниках, каждый из которых находится в своем состоянии (в точке с определенными значениями координат и проекций импульса в определенный момент времени).
Теперь перейдем к термодинамической системе, состоящей из N числа частиц. Введем для ее описания пространство состояний или фазовое пространство, в котором количество переменных состояния равно 6N (три координаты каждой частицы и три проекции импульса). Таким образом, фазовое пространство ТС становится 6N – мерным. Точка (фазовая точка) в этом пространстве будет однозначно определять состояние системы в определенный момент времени. Переход системы из одного (начального) состояния в другое (конечное) будет называться фазовой траекторией. Фазовые траектории не пересекаются и их совокупность ведет себя как несжимаемая жидкость. Примем без доказательства, что фазовые точки неуничтожимы и тогда непрерывность фазовых траекторий позволяет выбрать в системе физически бесконечно малый объем, форма которого с течением времени может изменяться, а размеры этого фазового объема остаются неизменными. Последнее утверждение для классических систем, в основе которых лежит механическое движение, было доказано Лиувиллем и носит название: «теорема Лиувилля», которую можно записать следующим образом: dV0 = dVt. Это означает, что элементарный объем сохраняется. Индексы 0 и t обозначают начальный и конечный моменты времени наблюдения системы. Теорема Лиувилля позволяет относиться к фазовым траекториям так же, как в механике к траекториям движения материальной точки и использовать математические методы дифференциального и интегрального исчисления для прогнозирования поведения системы.
При переходах от точки к точке в фазовом пространстве, каждой траектории можно, как и в примере с осциллятором, поставить в соответствие отдельную систему с такими же свойствами и тогда для любой измеряемой переменной состояния среднее значение переменной, вычисленное по времени для одной системы, должно совпадать со средним значением этой переменной, вычисленной по совокупности тождественных систем. В общем виде, обозначая любую переменную буквой F, можно кратко записать: <F(по времени)> = <F(по пространству или по ансамблю (совокупности тождественных систем)>, где скобки < > обозначают процедуру усреднения. Это свойство системы является следствием ее эргодичности, то есть способности фазовых траекторий подходить сколь угодно близко к любой точке фазового пространства. Равенство, выделенное жирно в тексте называют эргодической гипотезой, так как в общем виде для любых систем это утверждение не доказано.
При расчете средних значений переменных состояния системы выясняется, что состояние системы устойчиво, если средние значения долго не меняются с течением времени. Такие состояния называют равновесными. Поэтому средние значения переменных состояния характеризуют всю систему и определяют «макросостояние системы» в отличии от мгновенных значений переменных состояния, определяющих микросостояние системы. Мгновенные значения переменных (микропараметры), в свою очередь, могут быть заменены на совокупность тождественных систем, среднее значение переменных, вычисленное по этой совокупности, также должно определять макросостояние системы. Следовательно, каждому макросостоянию системы соответствует определенный набор микросостояний и такой же набор тождественных систем, который называют статистическим ансамблем.
Как мы говорили выше, отход от механики начинается тогда, когда невозможно точно определить значение переменных, поэтому для системы, состоящей из молекул (микрообъектов) следует воспользоваться понятием «хаоса», как такого состояния, для которого переменные становятся случайными величинами и точной траектории в фазовом пространстве не существует. В этом случае, система из начального состояния совершает несколько случайных шагов, пока не перейдет в конечное состояние. Говорят, что система «блуждает» в фазовом пространстве и переходы из одной точки пространства в другую характеризуются вероятностями. Марковым была доказана теорема, которую математически можно записать следующим образом: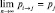 
, где pi→j характеризует вероятность перехода системы из i-го состояния в j-е состояние, pj – вероятность j-го состояния, а n – число шагов за которое система совершает переход. Из теоремы следует, что при большом числе шагов вероятность перехода определяется только вероятностью конечного состояния и не связана с начальным состоянием. Соответственно, вероятность обратного перехода из j-го состояния в i-е состояние будет определяться только вероятностью i-го состояния. Если вероятность i-го состояния слишком мала, то обратный переход в реальном времени практически не совершается (не наблюдается). Появляется необратимость процессов, происходящих в термодинамической системе. Система «забывает» начальные условия, поэтому применять к ней подход классической механики, становится неправомерным.
Рассмотрим простой пример, подтверждающий отличительные свойства термодинамической системы от системы механической. При заполнении пустого сосуда газом, молекулы можно впустить через различные отверстия в сосуде, осуществляя таким образом, различия в начальных условиях (рис. 26). Конечное же состояние во всех случаях будет одно и то же, так как один моль газа равномерно заполнит весь сосуд, и далее макропараметры его не будут меняться – газ придет в равновесное состояние. Очевидно, что это состояние является наиболее вероятным.
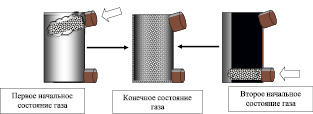
Рис. 26. Два различных варианта перехода газа из неравновесных состояний в равновесное состояние (в центре)
Таким образом, следствиями теоремы Маркова являются: первое – доказательство необратимости процессов в ТС и второе – ограниченность применения классической механики для описания ТС.
Если, какому-либо макросостоянию системы соответствует одно или небольшое число микросостояний, то система не будет долго в нем находиться при случайном блуждании, то есть это состояние будет характеризоваться малой вероятностью. Если же другому макросостоянию будет соответствовать огромное число микросостояний, то система будет находиться в нем долго, до тех пор, пока не побывает во всех этих микросостояниях. Отсюда можно сделать вывод, что равновесному состоянию, длящемуся очень долго, должно соответствовать огромное число микросостояний и, соответственно, наибольшая вероятность.
Для количественного описания состояния ТС введем два определения.
1. Определение. Набор микросостояний, соответствующих определенному макросостоянию, называют статистическим ансамблем.
2. Определение. Количество микросостояний или количество систем в статистическом ансамбле, соответствующих определенному макросостоянию, называют термодинамической вероятностью этого состояния. Будем обозначать термодинамическую вероятность следующим образом: WT. От обычной вероятности p ≤ 1, определенной в теории вероятностей, термодинамическая вероятность отличается тем, что она всегда не меньше единицы (в отличии от величины WT ≥ 1).
Так как для описания термодинамической системы требуется вероятностный подход, каждая переменная состояния системы становится случайной величиной, для которой закономерно распределение вероятностей. Среди всех возможных состояний ТС одно является наиболее вероятным – это равновесное состояние, поэтому для него можно использовать условие максимума: WT → WTmax, а следовательно, в равновесии
dWT = 0. (2.1.1)
Начнем анализ с классических распределений.