
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 2.2. Модель распределения молекул идеального газа по объему
Пусть большое количество молекул газа N, в рассмотренном выше примере (рис. 26) в конечном состоянии распределился по объему. Если известна величина объема сосуда V, можно вычислить вероятность попадания n числа молекул из N в произвольно выбранный небольшой объем ω, находящийся внутри сосуда. Будем решать задачу при условии, что газ является идеальным и отсутствует сила тяжести, действующая на молекулы.

Рис. 27. Сосуд с газом
В этом случае все точки объема сосуда являются равноправными и объем ω << V можно выбрать в любом месте сосуда (рис. 27). Так как движение молекул хаотично, количество молекул n является случайной величиной, для которой найдем распределение P(n). Мысленно пронумеруем все молекулы и тогда вероятность попадания молекулы № 1 в объем ω будет равна 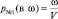 ; вероятность попадания двух первых по номеру молекул в объем ω (по теореме умножения вероятностей) будет равна
; вероятность попадания двух первых по номеру молекул в объем ω (по теореме умножения вероятностей) будет равна 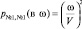 . Наконец, вероятность попадания от первой по номеру молекулы до n-й в объем ω окажется равной
. Наконец, вероятность попадания от первой по номеру молекулы до n-й в объем ω окажется равной 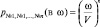 . Остальные молекулы газа не должны попасть в выбранный объем. Вероятность этого события по аналогии с предыдущими вариантами будет равна
. Остальные молекулы газа не должны попасть в выбранный объем. Вероятность этого события по аналогии с предыдущими вариантами будет равна
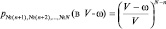 .
.
Для того, чтобы только n первых по номеру молекул попали в выбранный объем, должны выполняться два последних события совместно с вероятностью, равной произведению вероятностей этих событий:
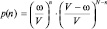 .
.
Для расчета вероятности попадания любых n молекул, а не только первых по номеру, в выбранный объем, необходимо сложить вероятность p(n) столько раз, сколько существует вариантов выбора n молекул с неповторяющимися номерами из общего числа N. Из комбинаторики известно, что это количество определяется сочетаниями из N по n. Тогда окончательно будем иметь:
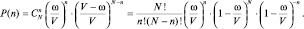
Для того чтобы вести расчет только через количество молекул, введем параметр распределения m – как такое количество молекул, которое пропорционально выбранному объему ω. Тогда полному объему V будет соответствовать полное число частиц N и можно от отношения объемов перейти к отношению чисел молекул: 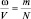 . Полученное выше распределение можно упростить, считая, что, во-первых, в пределе
. Полученное выше распределение можно упростить, считая, что, во-первых, в пределе  и, во-вторых, справедлива формула приближенного вычисления Стирлинга для
и, во-вторых, справедлива формула приближенного вычисления Стирлинга для 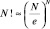 (см. справочники по математике). Тогда получим для P(n) следующее выражение:
(см. справочники по математике). Тогда получим для P(n) следующее выражение:
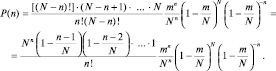
Переходя к пределу при N → ∞ и используя один из «замечательных пределов», в итоге получим:
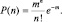 (2.2. 1)
(2.2. 1)
Формула (2.2.1) была впервые получена Пуассоном и называется распределением Пуассона.
Среднее значение числа молекул, попавших в выбранный объем, вычисляется по обычной формуле расчета среднего значения дискретной случайной величины и дает ответ: 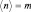 , то есть среднее значение совпадает с введенным параметром распределения Пуассона. Вероятность n – среднего, вычисленная по распределению (2.2.1), оказывается (в пределе при N → ∞) близка к единице, то есть является самой большой вероятностью. Поэтому можно сделать вывод, что наиболее вероятно такое событие, для которого в любом объеме встретится среднее число молекул, пропорциональное размерам выбранного объема. Из этого вытекает, что газ распределен по сосуду равномерно (молекулярный «хаос»). Следует понимать, что по теореме полной вероятности, вероятность равная единице может быть только для суммы всех событий, что в статистике определяет условие нормировки.
, то есть среднее значение совпадает с введенным параметром распределения Пуассона. Вероятность n – среднего, вычисленная по распределению (2.2.1), оказывается (в пределе при N → ∞) близка к единице, то есть является самой большой вероятностью. Поэтому можно сделать вывод, что наиболее вероятно такое событие, для которого в любом объеме встретится среднее число молекул, пропорциональное размерам выбранного объема. Из этого вытекает, что газ распределен по сосуду равномерно (молекулярный «хаос»). Следует понимать, что по теореме полной вероятности, вероятность равная единице может быть только для суммы всех событий, что в статистике определяет условие нормировки.
