Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 2.3. Распределение молекул идеального газа по проекциям скоростей
Фазовое пространство координат и импульсов системы идеального газа можно представить разбитым на подпространства, одно из которых связано только с координатами, а другое, только с импульсами молекул.
Поставим задачу поиска распределения по импульсам, считая эту переменную состояния случайной величиной. Будем далее рассматривать поведение отдельной молекулы, совершающей случайное «блуждание» в импульсном подпространстве. Это позволит перейти от 3N-мерного к 3-хмерному подпространству одной молекулы. Наконец, считая все молекулы тождественными микрообъектами, можем далее перейти от подпространства импульсов к 3-хмерному пространству проекций скоростей (рис. 28). Для этого нужно просто ввести масштабный множитель для каждой проекции импульса: vx = px/m; vy = py/m; vz = pz/m. Если будет найдена вероятность обнаружения у произвольно выбранной молекулы определенных значений проекций скоростей, то в соответствии с частотным определением вероятности, полученная вероятность будет означать долю молекул газа с теми же значениями проекций скоростей, что и у отдельной молекулы. Таким образом, будет получено описание газа «в целом». Выберем в пространстве скоростей элементарный объем dVv в окрестности точки, определяемой направлением l, образованный элементарными проекциями: dvx, dvy, dvz. Тогда dVv = dvx + dvy + dvz, а величина скорости в выбранном направлении будет равна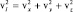 
.
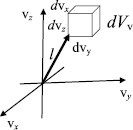
Рис. 28. Элементарный объем в пространстве скоростей
Появление у произвольно выбранной молекулы газа проекции скорости vl есть событие сложное. Оно заключается в том, что она одновременно получила и проекцию скорости vx, и проекцию скорости vy, и проекцию скорости vz . Тогда по теореме умножения вероятностей совместных событий можно записать: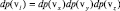 
. Вероятности dp малы потому, что размеры интервалов в которые они попадают являются также физически бесконечно малыми величинами dv.
Каждой величине проекции скорости соответствует однозначно только одна величина квадрата скорости (обратное неверно), а вероятности при этом остаются прежними. Действительно, если например, на гранях кубика в качестве случайной величины написать числа от 1 до 6, а затем перейти к квадратам этих величин, то значения случайных величин изменятся, а вероятности их появления, определяемые количеством граней, останутся прежними. Поэтому частоты встречаемости величины проекции скорости и ее квадрата одинаковы и можно записать равенство:
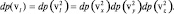
Выразим распределение вероятностей в виде функции плотности вероятности. Тогда запишем:
.
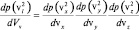Откуда следует:
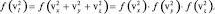
Единственная из элементарных функций, удовлетворяющая последнему равенству, является показательная функция. Выберем в качестве основания в показательной функции величину e – основание натуральных логарифмов. Тогда, в общем виде, распределения по проекциям скоростей могут быть представлены следующим образом:
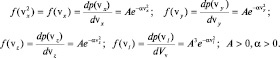(2.3.1)
Функции в формулах (2.3.1) были впервые получены Максвеллом и называются распределениями Максвелла по проекциям скоростей. Так как все направления в газе равноправны, то нормирующие множители А выбраны по всем направлениям одинаковыми. Знак минус перед константой α в показателях функций поставлен потому, что для любой функции плотности распределения вероятностей должно выполняться условие нормировки: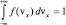 
, а при положительном показателе в функции распределения интеграл не имеет конечного предела.
Первые три функции распределения (формулы (2.3.1)) показывают: с какой вероятностью у произвольно выбранной молекулы газа можно обнаружить величину соответствующей проекции скорости, попадающей в единичный интервал проекций скоростей.
Последняя функция (2.3.1) показывает: с какой вероятностью у произвольно выбранной молекулы газа можно обнаружить проекцию скорости на направление l, попадающую в единичный объем пространства скоростей.
Для построения графиков функций (2.3.1) вычислим нормирующий множитель А из условия нормировки.
,
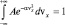откуда следует
.
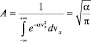Тогда, функция распределения по проекциям в направлении l будет записана следующим образом:
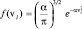(2.3.2)
Исходя из геометрического смысла определенного интеграла, условие нормировки характеризует всю площадь под кривой функции плотности вероятности (рис. 29), а также полную вероятность того, что у произвольно выбранной молекулы можно обнаружить все равно какую величину проекции скорости в интервале от –∞ до +∞ значений проекций скоростей.
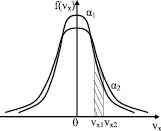
Рис. 29. Графики распределений по проекциям скоростей молекул
По размерам площади можно оценивать вероятности того, что у произвольно выбранной молекулы газа величина проекции скорости окажется в интервале от vx1 до vx2 (см. заштрихованную площадку на рис. 29).