
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 2.5. Классическая статистика. Распределение Максвелла-Больцмана
Пусть мы имеем систему, состоящую из большого числа N классических частиц, которые распределены по 6-мерному фазовому пространству. Каждая из них займет определенное место в пространстве состояний и газ «в целом» сконцентрируется вблизи средних значений переменных состояния в некотором фазовом объеме. Разобьем фазовое пространство на одинаковые по размерам ячейки и будем считать, что попадание нескольких частиц в любую ячейку приводит к их физической неразличимости по переменным состояния. Теперь каждому микросостоянию будет соответствовать одна ячейка, а макросостоянию – весь предоставленный системе объем из k ячеек. Макросостояние, определяемое средними величинами переменных состояния, не будет меняться до тех пор, пока частицы не выходят за рамки объема, занятого системой. Микросостояния системы меняются только при перестановке частиц по k ячейкам. Перестановки частиц внутри каждой ячейки не меняют микросостояния, так как по переменным состояния они считаются неразличимыми.
При таком подходе, предложенном Больцманом и получившем название «метода ячеек Больцмана», легко подсчитать термодинамическую вероятность макросостояния системы. Если бы каждой частице соответствовала только одна ячейка, то количество микросостояний системы определялось бы всеми перестановками частиц N!. Но так как в одну ячейку может попасть несколько частиц, то общее число микросостояний уменьшается в n1! раз за счет неразличимости частиц в первой ячейке, в n1! раз за счет неразличимых перестановок частиц во второй ячейке и т.д. до nk! раз перестановок в k-й ячейке. Поэтому, окончательно, термодинамическая вероятность, определяемая числом различных микросостояний, будет равна
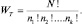 (2.5.1)
(2.5.1)
Каждой ячейке ni соответствует величина энергии εi, поэтому, зная распределение частиц по ячейкам, можно найти их распределение по состояниям с энергиями εi. Будем исследовать газ в состоянии равновесия, то есть при условии (2.1.1): dWT = 0. Так как величина термодинамической вероятности всегда не меньше единицы, то можно перейти к логарифму этой вероятности, условие максимума которого будет совпадать с условием максимума самой величины WT. Тогда имеем новое условие равновесия системы: d(lnWT) = 0. Используя его и формулу (2.5.1), получим:
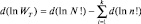 .
.
Будем считать, что количество частиц в любом микросостоянии велико и справедлива формула Стирлинга: 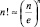 . Тогда можно записать (при N! = const) следующее выражение:
. Тогда можно записать (при N! = const) следующее выражение:
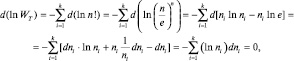
откуда следует
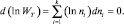 (2.5.2)
(2.5.2)
При равенстве нулю правой части знак минус перед суммой можно опустить. При поиске распределения, кроме условия равновесия d(lnWT) = 0 необходимо учесть также, что не меняется полное число частиц и полная энергия системы. Тогда dN = 0 и dE = 0. Для объединения всех трех условий в одном равенстве, воспользуемся методом неопределенных множителей Лагранжа и сложим три последних равенства:
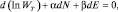 (2.5.3)
(2.5.3)
где α и β – неопределенные множители Лагранжа, подобранные таким образом, чтобы суммировались безразмерные величины. Так как 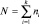 и
и 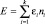 , то
, то 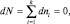 а
а 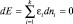 .
.
Подстановка полученных равенств и результатов из (2.5.2) в (2.5.3) приводит к следующему уравнению:
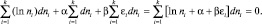
которое представляет собой сумму ряда с коэффициентами, стоящими в квадратных скобках, и независимыми переменными dni. Как известно из математики, сумма такого ряда равна нулю тогда и только тогда, когда при каждом независимом переменном dni коэффициент обращается в нуль. Поэтому можно записать: ln dni + α + βεi = 0, откуда следует: 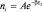 – число частиц в ячейке с энергией εi, состоящей из потенциальной εП и кинетической энергии εК. Каждая ячейка представляет собой элементарный объем фазового пространства, поэтому полученное равенство после деления слева и справа на N >> ni будет характеризовать относительно малую долю частиц (или вероятность обнаружения частицы) с энергией εi, в единичном объеме фазового пространства:
– число частиц в ячейке с энергией εi, состоящей из потенциальной εП и кинетической энергии εК. Каждая ячейка представляет собой элементарный объем фазового пространства, поэтому полученное равенство после деления слева и справа на N >> ni будет характеризовать относительно малую долю частиц (или вероятность обнаружения частицы) с энергией εi, в единичном объеме фазового пространства:
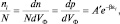
где 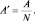 (2.5.4)
(2.5.4)
Каждая частица одновременно находится и в координатном (с вероятностью dp1 в dVкоорд) и импульсном (с вероятностью dp2 в dVимп) подпространствах, поэтому можно разбить полученное распределение на два независимых распределения по координатному и импульсному подпространствам:
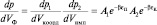 , (2.5.5)
, (2.5.5)
где A′ = A1A2, ε = εП + εК.
Выделим вначале ту часть распределения, которая связана с кинетической энергией и характеризует вероятность обнаружения у произвольно выбранной частицы кинетической энергии, попадающей в единичный объем пространства импульсов (скоростей). Сравним его с распределением Максвелла (правая формула в (2.4.5)).
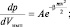
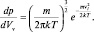 (2.5.6)
(2.5.6)
Из сравнения видно, что 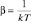 , так как вид функций одинаков с точностью до нормирующего множителя.
, так как вид функций одинаков с точностью до нормирующего множителя.
Теперь рассмотрим первое распределение из (2.5.5) и учтем, что элементарный объем фазового координатного подпространства – это, по сути, элементарный объем обычного трехмерного пространства, выделенный из полного объема V, предоставленного частицам системы. Так как величина константы β в распределениях по координатному и импульсному пространству одна и та же, запишем первую функцию распределения следующим образом:
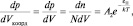 (2.5.7)
(2.5.7)
откуда
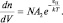
Переходя в формуле (2.5.7) к концентрации частиц 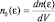 , будем иметь:
, будем иметь:
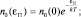 n0(0) = NA2. (2.5.8)
n0(0) = NA2. (2.5.8)
Функции (2.5.7) и (2.5.8) представляют собой распределения, которые называют распределениями Больцмана. Функцию в (2.5.4) называют распределением или статистикой Максвелла-Больцмана.
Рассмотрим два примера использования распределения Больцмана для решения конкретных физических задач.
1. Применим распределение Больцмана (2.5.8) к атмосфере Земли.
В этом случае εП = mgh, где m – масса отдельной молекулы; g – ускорение свободного падения и h – высота слоя воздуха, отсчитываемая от поверхности Земли (на уровне моря, при h = 0). Переходя от концентрации молекул к давлению (p = n0kT), после умножения в формуле (2.5.8) слева и справа на kT, получим формулу закона Торичелли для давления в атмосфере на высоте h:
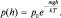
Таким образом, распределение Больцмана, в частном случае, провело к известному, экспериментально проверенному закону.
2. Используя распределение Больцмана можно обосновать гипотезу Эйнштейна о существовании индуцированного излучения атомов.
Возникновение квантовой механики, как известно из истории физики, связано с изучением спектра излучения черного тела, состоящего из атомных осцилляторов, расположенных в стенках черного тела и фотонов, находящихся внутри объема в состоянии теплового равновесия. Потери энергии на излучение компенсируются внешним источником. Можно считать систему замкнутой, если энергию в процессе излучения и работу внешнего источника считать малыми по сравнению с полной энергией системы. Тем не менее, интенсивность излучения I(ν), то есть среднее количество вылетающих фотонов за единицу времени, пропорциональна их количеству в системе.
Планком была получена формула распределения средней энергии по спектру равновесного излучения черного тела, в основе которой лежит функция 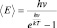 . Так как
. Так как 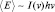 , то
, то
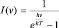 . (2.5.9)
. (2.5.9)
Выделим в системе такие стационарные состояния атомов, на которых происходит излучение. Поглощение и излучение фотонов в среде атомами при непрерывном излучении (T = const) должно подчиняться принципу детального динамического равновесия: вероятности переходов атомов из невозбужденного в возбужденное состояния и обратно должны быть равными WI→II = WII→I.
Этот же принцип работает при равновесии в замкнутой системе «пар-жидкость» (в состоянии насыщения): количество переходов и вероятность перехода отдельных молекул из пара в жидкость и обратно за реальное время одинаковы.
Вероятность перехода из первого (невозбужденного) состояния во второе (возбужденное) состояние пропорциональна числу атомов в стенках черного тела, находящихся в невозбужденном состоянии и количеству фотонов в полости, способных перевести атомы в возбужденное состояние. Считалось, что обратный переход происходит спонтанно, не нуждается в фотонах и поэтому вероятность этого перехода пропорциональна только количеству атомов в возбужденном состоянии. Можно записать условие равновесия:
I(ν)NI = NII, (2.5.10)
откуда имеем: 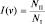 . Используя формулу распределения Больцмана (2.5.8), получим:
. Используя формулу распределения Больцмана (2.5.8), получим:
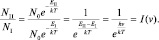
Видим, что полученный результат не соответствует формуле Планка (2.5.9), а следовательно, и экспериментальным данным.
Используем формулу Планка для того, чтобы из нее получить условие равновесия в системе. Заменим по формуле Больцмана величину 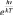 на отношение
на отношение 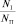 и подставим в (2.5.9):
и подставим в (2.5.9):
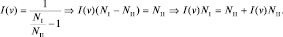
Полученный результат возвращает к условию равновесия в системе: левая часть равенства определяет переход из невозбужденного состояния в возбужденное, а правая часть – обратный переход. При этом, в правой части появилось дополнительное слагаемое (сравните с (2.5.10)), которое показывает, что при переходе из возбужденного состояния в невозбужденное возможен не только спонтанный переход, но и вынужденный переход под действием фотонов. Этот переход и был назван Эйнштейном «индуцированным».
Начиная со следующей лекции, рассмотрим статистики квантовых частиц.
