Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

СТАТИСТИЧЕСКИЕ МОДЕЛИ В КВАНТОВОЙ ФИЗИКЕ ЭКОЛОГИИ И ЭКОНОМИКЕ

Рау В. Г., Рау Т. Ф., Малеев А. В.,

§ 2.7. Квантовая статистика бозонов. Распределение Бозе-Эйнштейна

Как мы определили выше, к классу бозонов относятся частицы, для которых не выполняется принцип запрета Паули, имеющих целый спин (или нулевой), с симметричной Ψ-функцией состояния. Из реальных частиц к бозонам относятся некоторые ядра, элементарные частицы: фотоны, пионы (π-мезоны) и др., а также квазичастицы: фононы, экситоны, магноны.

Фундаментальной моделью бозонной термодинамической системы является фотонный газ в абсолютно черном теле. Рассмотрим равновесное состояние такой системы. В качестве простого примера представим распределение трех бозонов Ni по трем ячейкам Zi с энергией εi. Будем иметь таблицу перестановок бозонов (рис. 39) для расчета термодинамической вероятности i-го состояния wТi, комбинаторно записываемую следующим образом:

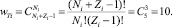(2.7.1)

Рис. 39. Десять перестановок трех бозонов по трем состояниям

Пусть система находится в k-состояниях с энергиями εi (i = 1, 2, ..., k), каждое из которых, соответственно, характеризуется вероятностями wT1, wT2, ..., wTk. Тогда термодинамическая вероятность всей системы запишется в виде произведения вероятностей всех состояний 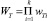. Найдем распределение вероятностей в зависимости от величины энергии каждого состояния. В равновесии величины WT и lnWT максимальны, поэтому условие равновесия системы можно записать следующим образом:

d(lnWT) = 0. (2.7.2)

Произведем операцию дифференцирования при условии, что количество частиц Ni и состояний Zi велики, поэтому можно использовать формулу Стирлинга для вычисления факториалов больших чисел:

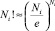и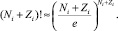

Для упрощения записи, при расчетах, единицей пренебрежем по сравнению с числом частиц (2.7.1):

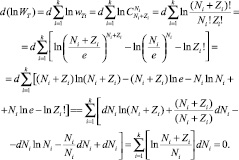(2.7.3)

При вычислениях, производимых в (2.7.3) было учтено, что дифференциал от постоянных величин Zi и lnZi! равен нулю, так как количество состояний с энергией εi не меняется, а меняется лишь число частиц в ячейках.

Кроме условия равновесия для системы должно выполняться еще два условия: первое, неизменность количества частиц в системе и постоянство величины полной энергии системы: 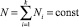и .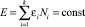

Воспользовавшись далее методом Лагранжа неопределенных множителей α и β, запишем в виде системы уравнений условие равновесия (2.7.3), условия сохранения полного числа частиц и полной энергии следующим образом:

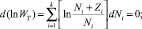
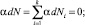
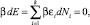
откуда, после суммирования этих трех равенств, имеем:

.

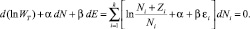Сумма образовавшегося ряда равна нулю тогда и только тогда, когда при каждой i-й переменной коэффициенты ряда, записанные в квадратной скобке, обращаются в нуль. Поэтому можно записать следующее равенство:

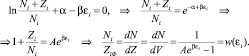(2.7.4)

Полученная функция характеризует распределение частиц – бозонов по состояниям с энергией ε. Из принципа соответствия между классическими частицами и микрообъектами, по аналогии с тем, как это было сделано при выводе распределения для фермионов (§6), получим величину неопределенного множителя 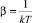. Полная функция распределения по энергиям, как это рассматривалось выше в §6 (2.6.6), должна состоять из распределения состояний по энергиям и распределения частиц по состояниям. Окончательно запишем:

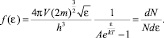(2.7.5)

Выведенное распределение для частиц с целым ненулевым спином называется распределением Бозе – Эйнштейна. Для бозонов с нулевым спином, число состояний у которых в два раза меньше из-за отсутствия спина, получим еще одно распределение:

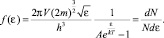(2.7.6)

Равенство (2.7.6) также является распределением Бозе – Эйнштейна.

В качестве примера применим полученное распределение к термодинамической системе, модель которой называют абсолютно черным телом. В стенках черного тела находятся атомные осцилляторы, излучающие и поглощающие энергию электромагнитного поля порциями – квантами, что послужило Эйнштейну основанием считать «кванты» самостоятельными частицами. Эти частицы, названные позже фотонами, образуют в полости черного тела фотонный газ. Напрямую применить к этому газу статистику Бозе – Эйнштейна (2.7.6) некорректно, так как масса покоя фотона равна нулю и величина его импульса определяется через полную энергию следующим образом: p = ε/c, где с – скорость распространения света в вакууме. Поэтому пересмотру подлежит вывод распределения ячеек фазового пространства фотонного газа по энергиям (формула (2.6.6)). Полное число ячеек (с учетом спина фотона), предоставленное системе, запишем следующим образом:

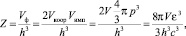
откуда после взятия производной по энергии, получим z(ε):

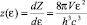(2.7.7)

Теперь перейдем к распределению частиц по энергиям, перемножив распределения частиц по состояниям w(ε) (2.6.6) и состояний по энергиям z(ε):

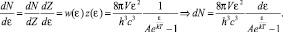(2.7.8)

Умножая энергию отдельного фотона ε = hv на количество фотонов с той же частотой dN(v) найдем их энергию dE(v) = εdN. После замены переменной энергии на частоту в формуле (2.7.8), получим:

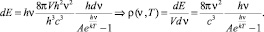(2.7.9)

Выражение (2.7.9) является формулой Планка для объемной спектральной плотности энергии излучения в спектре абсолютно черного тела (рис. 40), если положить A = 1.

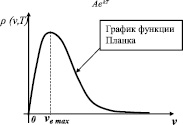
Рис. 40. Вид функции распределения Планка

При объяснении спектра излучения черного тела на основе классических представлений, Рэлей рассчитал спектральную плотность стоячих электромагнитных волн и получил функцию 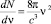. Умножая на величину средней энергии стоячей волны 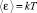, получаем формулу Рэлея для спектра излучения черных тел 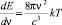. Очевидна аналогия с формулой Планка (2.7.9). Различие заключается в том, что средняя энергия квантового осциллятора не равна kT, а определяется формулой:

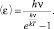(2.7.10)

Вопрос о величине коэффициента А в распределении Бозе –Эйнштейна является не простым вопросом. Как это рассмотрено выше, величина А вычисляется следующим образом: 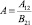, то есть зависит от отношения коэффициентов Эйнштейна, а поэтому численно может быть не равна единице. Это принципиально отличает статистику бозонов от статистики фермионов.

Явления сверхтекучести и сверхпроводимости связаны как со статистикой фермионов, так и бозонов, поэтому рассмотрим основные физические принципы, лежащие в основе этих явлений.

Явление сверхтекучести вещества было открыто в 1938 г. П. Капицей для смеси изотопов 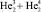при температуре T ≈ 2 K. Часть жидкости легко, не образуя капель и разрывов, как единое целое проходила через капилляры без вязкого трения. Простейший эксперимент, демонстрирующий связанное состояние жидкости, представим следующим образом. Если из сосуда начать под наклоном выливать эту жидкость, то, вернув сосуд в вертикальное состояние, можно наблюдать, как жидкость продолжает вытекать, вытягивая из сосуда остальную часть жидкости. Упрощенную механическую модель связанного состояния жидкости легко предложить, если в качестве вещества избрать длинную металлическую цепочку, поместив ее в сосуд. Свесившийся конец цепочки вытянет всю остальную часть цепочки.

Рассмотрим эксперимент с точки зрения статистики бозонов. Анализируя функцию распределения (1.9.4), можно допустить, что величина константы А становится меньше единицы, а 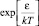, которая всегда положительна, при низких температурах стремится к единице. Тогда возможна ситуация при которой произведение 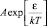будет меньше единицы. В этом случае производные 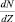и 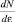становятся отрицательными, но так как количество ячеек в фазовом пространстве dZ и интервал энергии dε положительны, приходится констатировать, что dN < 0. Тогда и 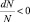, а это означает, что некоторая доля частиц бозонного газа перестала быть объектом статистики, нарушилась гипотеза элементарного беспорядка, появилось упорядоченное состояние. Другими словами, при определенных условиях произошел фазовый переход, и некоторая доля бозонов перестала подчиняться законам хаотического движения, стала двигаться согласованно, то есть конденсировалась в общее связанное состояние. Говорят, что образовался «бозе-конденсат».

Явление сверхпроводимости было открыто Камерлинг-Оннесом в1911году и заключалось в том, что при температуре около 4 К удельное сопротивление проводника (в опытах Камерлинг-Оннеса это была ртуть) становилось равным нулю. Классическая физика не могла найти объяснения этому явлению и только после создания квантовой электродинамики, открытия сверхтекучести вещества и анализа статистики бозонов и фермионов Бардиным, Купером и Шриффером (теория БКШ) было найдено решение проблемы.

Сложность применения фермионной статистики электронного газа, определяющего проводимость металлов, к объяснению явления сверхпроводимости по аналогии со сверхтекучестью наличием конденсированного состояния частиц, оказалось неправомерным. Действительно, в статистике Ферми-Дирака (формулы (2.6.7) и (2.6.14)), производные 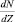и 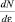не могут быть отрицательными ни при каких условиях из-за отсутствия минуса перед единицей, стоящей в знаменателе функции распределения. Конденсироваться в какое-либо одно состояние электроны не могут, так как частицы с полуцелым спином подчиняются принципу запрета Паули. Первым шагом в теории БКШ было использование условия квантования поля в применении к твердому телу, как к сплошной среде. Так же как электромагнитная волна может быть представлена в виде потока движущихся фотонов, распространение возмущения в сплошной среде представляющее собой волновой процесс (звуковые волны), можно «проквантовать», то есть представить в виде движущихся частиц. Эти частицы были названы фононами (фонос (греч.) – звук), в отличии от фотонов (фотос (греч.) – свет).

Еще одной особенностью фононов является невозможность их самостоятельного существования в отрыве от среды. Такие объекты названы квазичастицами. Хаотические колебания ионов в узлах кристаллической решетки металлов создают хаос в движении фононов и можно говорить о фононном газе, который, как и фотонный газ, подчиняется бозонной статистике. При низких температурах амплитуды колебаний ослабляются, и некоторые ионы могут попадать в своеобразный резонанс, то есть могут начать колебаться согласованно. Эта ситуация похожа на согласованное резонансное движение некоторых математических маятников на одной струне, когда по ней распространяются колебания, идущие от одного из маятников, как от источника.

Взаимодействие ионов с электронами на квантовом языке представляется как электрон-фононное взаимодействие. Низкие температуры обуславливают передачу согласованных колебаний ионов электронам с помощью фононов. При этом энергетические состояния электронов также согласуются. Но, согласованные состояния электронов возможны только в том случае, когда у них отличается хотя бы одно квантовое число. В результате, связанными оказываются два электрона с различными спинами. Образовавшаяся пара связанных электронов, названная «куперовской парой» обладает суммарным спином, равным нулю, то есть может служить объектом бозонной статистики, для которой не работает принцип Паули. Образуется бозе-конденсат, состоящий из куперовских пар. Под действием внешнего поля куперовские пары образуют направленное движение зарядов, то есть электрический ток в сверхпроводнике. Итак, сверхпроводимость это сверхтекучесть куперовских пар.

В 1986 г. Беднорц и Мюллер обнаружили способность керамики на основе оксидов меди, лантана и бария (La2-xBaxCuO4) переходить в сверхпроводящее состояние при 30 К. Важнейшей чертой открытия высокотемпературных сверхпроводников можно назвать то, что сверхпроводимость была обнаружена не у традиционных интерметаллидов, органических или полимерных структур, а у оксидной керамики, обычно проявляющей диэлектрические и полупроводниковые свойства. Это позволило в течение короткого времени создать почти одновременно в США, Японии, Китае и России новые, более совершенные поколения структур металлоксидных сверхпроводников.

В феврале 1987 г. была синтезирована сверхпроводящая керамика из оксидов бария, иттрия и меди YBa2Cu3O7-x с критической температурой 93 К, то есть выше точки кипения жидкого азота. В 1988г. синтезирована серия соединений Bi2Sr2Can-1CunO2n + 4, среди которых фаза с n = 3 имеет Tc = 108 K. Приблизительно в это же время получен сверхпроводник Ti2Ba2Ca2Cu3O10 c Tc = 125 K. В 1993 г. Антипов, Путилин и др. открыли ряд ртутьсодержащих сверхпроводников. В настоящее время фаза HgBa2Ca2Cu3O8+d имеет наибольшее известное значение критической температуры (135 К), причем при внешнем давлении 350 тысяч атмосфер температура перехода в сверхпроводящее состояние возрастает до 164 К.