Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 3.1. Моделирование случайных событий в экологической системе
Представим широко известную задачу о травоядных и хищниках в единой экосистеме, когда неограниченной остается только пища для травоядных. Количество последних будет возрастать естественным путем, но и одновременно уменьшаться при «встрече» с хищником. Каждую такую встречу будем считать случайным событием. Вероятность таких встреч пропорциональна как числу N – травоядных, так и M – хищников, поэтому уравнение для скорости изменения количества травоядных запишется следующим образом:
.
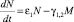Количество же хищников растет за счет «встреч» с травоядными. Тогда уравнение для скорости изменения количества хищников будет выглядеть так:
.
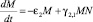Количество хищников, конкурирующих друг с другом за «пищу», уменьшается пропорционально их числу (первое слагаемое в правой части уравнения). Все вводимые коэффициенты пропорциональности имеют вероятностный смысл, а события случайны. Поэтому, несмотря на детерминированность (однозначность) решения самих систем уравнений, их интерпретация носит статистический характер.
Итак, система уравнений для переменных N и M примет следующий вид:
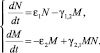(3.1.1)
Фазовый портрет на диаграмме в переменных N и M имеет стационарное решение, при котором не происходит изменения числа животных, т.е. N = N0 и M = M0. Это возможно, если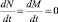 
. Тогда ε1N = γ1,2M и ε2M = γ2,1MN.
В фазовом пространстве это будет соответствовать точке с координатами (M0, N0) (рис. 41). Если равновесие нарушено, то рост числа травоядных (ab) способствует увеличению количества хищников (направление bc на диаграмме) c некоторым запаздыванием, затем число травоядных уничтожается хищниками (cd), но это приводит к уменьшению количества хищников и восстановлению первоначальных условий (da). Образовался замкнутый цикл.
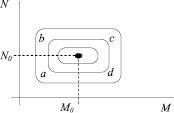
Рис. 41. Фазовая диаграмма системы «хищник-жертва»
При различных константах ε1, ε2, γ1,2 и γ2,1, циклические процессы имеют на диаграмме различные размеры. Полученный результат можно также изобразить на графиках M(t) и N(t) для одного из циклов при неизменных константах (рис. 42).
В литературе обычно приводится экспериментальная диаграмма изменений числа кроликов и рысей в Канаде за достаточно большой временной период. Вид графика хорошо согласуется с простой моделью процесса, рассмотренной теоретически.
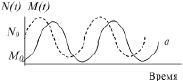
Рис. 42. Теоретические кривые в системе «хищник-жертва»
Открытые физические системы, так же давно и успешно изучаемые в синергетике, получили широкое распространение не только в физических науках, но и во всем естествознании. Основу их исследования составляют компьютерные модели, позволяющие решать системы нелинейных уравнений, иногда, не имеющие аналитических методов их решения. Вернемся к усложненной модели Лотки – Вольтерра («хищник – жертва»), рассмотренной выше:
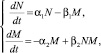(3.1.2)
где N – количество «кроликов-жертв» в системе с неограниченном резервом травяной пищи для них, а M – количество «рысей-хищников», рост которых зависит от вероятности встреч хищника с жертвой, которая пропорциональна произведению NM. Коэффициенты α1, α2, β1 и β2 в этой системе являются константами, а их смысл мы обсуждали выше. Теперь введем в коэффициенты β1 и β2 зависимость от времени и будем считать их связанными с функцией обучаемости ε(t) в виде
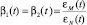
где εN(t) – обучаемость кроликов, а εM(t), соответственно, – обучаемость хищников.
Очевидно, что чем быстрее происходит обучаемость кроликов по сравнению с обучаемостью хищников, тем меньше величина β1(t) и β2(t), что в свою очередь приводит к благоприятным условиям «выживания» кроликов.
На рис. 43а представлены изменения популяций в зависимости от времени (три первых диаграммы, программа «MatCad») и фазовая траектория для величин N и M при
ε1(t) = ct2 + d и ε2(t) = at + b,
а на рис. 43б при
ε1(t) = ct + d и ε2(t) = at + b.
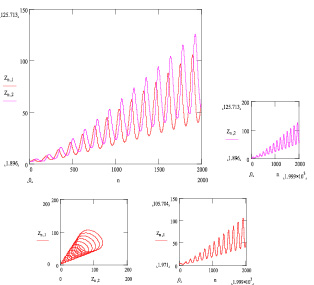
Рис. 43а. Результат решения системы (3.1.2) при ε1(t) = ct2 + d и ε2(t) = at + b
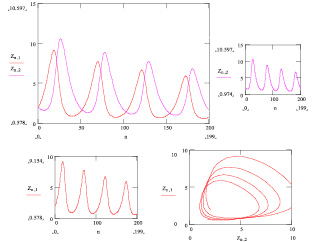
Рис. 43б. Результат решения системы (3.1.2) с параметрами ε1(t) = ct + d и ε2(t) = at + b