Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 3.4. Модель распределения вероятностей по доходам участников рынка
Рассмотрим следующую модель статистического распределения участников рынка (владельцев торговых точек) N по получаемым каждым из них доходом R, величина которого является случайной. В комплекс условий входит «однородность» рынка, которую можно предложить, выбрав, например «рынок продовольственный», или «книжный рынок», доходы от продаж у участников которого сопоставимы. Соответствующая доля участников с определенным доходом, приходящимся на единицу дохода (например, на 1 руб.) определит распределение частотной плотности вероятности. Это распределение при большой выборке или даже при полном опросе всех N участников может быть аппроксимирована некоторой функцией, позволяющей ответить на вопросы, возникающие при работе рынка.
Приведем конкретный пример работы небольшого продовольственного рынка по результатам выборки в разное время года, когда сезонная активность покупателей сказывается на распределении. Проводился месячный опрос участников рынка, результаты которого в виде гистограммы приведены на рис. 48. Наиболее часто встречаемый ежедневный доход, который в статистике называется модой, оказался близким к величине 400 руб. Размеры интервалов подбирались таким образом, чтобы в каждом интервале, начиная со второго, присутствовали данные не менее, чем 10 участников рынка. Вид гистограммы легко аппроксимируется графиком функции распределения, который подробно анализирует распределение для молекул идеального газа по скоростям (Статистика, Часть 1). Этот анализ, проведенный нами выше, проведем еще раз, заменив случайные величины скоростей молекул на случайные величины дохода частников рынка.
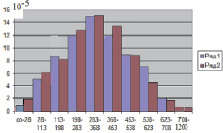
Рис. 48. Гистограмма распределения участников рынка по доходам
Запись функции распределения и основные характеристики распределения, полученные с учетом условия нормировки, должны соответствовать расчетам, проведенным нами ранее. В итоге имеем (3.4.1):
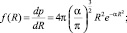
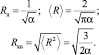(3.4.1)
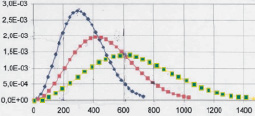
Рис. 49. Графики функции распределения по доходам при Rн = 300 руб.; Rн = 400 руб.; Rн = 600 руб.
Знание распределения позволяет построить функцию общего вида при различных значениях наиболее вероятной величины дохода (рис. 49):
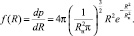(3.4.2)
В качестве закрепления материала, рекомендуется найти ответы на следующие вопросы.
1. Что показывает конкретная точка на графике по отношению к отдельному участнику рынка и ко всем участникам «в целом»?
2. Как по графику оценить долю участников, доходы которых попадают в интервал от R1 до R2?
3. Что показывает условие нормировки функции распределения?
4. Как изменится вид графика распределения при увеличении активности покупателей, или при ее понижении?