Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 3.5. Модель экономической системы межотраслевого баланса
Для описания операций в экономике рассмотрим в качестве математического языка – «язык» матриц. В конечном счете, взаимодействие экономических структур в системе, выраженное в матричной форме, позволяет давать обоснование самого факта рождения устойчивой системы. Именно межотраслевой баланс, как яркий пример экономической системы был впервые описан Леонтьевым на языке матриц.
Статистические, производственные показатели, а также расчеты, производимые на основе полученной информации, часто требуют сохранения результатов для их дальнейшего использования. В этом случае создаются числовые таблицы, в которых информация в той или иной степени упорядочена. В таблицу могут быть внесены характеристики элементов какого-либо множества, параметры состояния системы и порядок применения операций, так как и операции могут являться элементами определенных множеств (например, в теории групп симметрии – операции симметрии). Возникает проблема оптимального использования таблиц, то есть проблема операций (действий) с таблицами данных. Рассмотрим конкретные примеры.
Пусть, в простейшем случае, ежемесячные затраты из семейного бюджета Y складываются из трех основных видов товара ((Q1, Q2, Q3), приобретаемых в трех различных магазинах (Mj) по различным ценам (разного сорта). Количество товаров QЯ, купленных в январе и Qф, купленных в феврале, составят таблицы следующего вида:
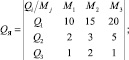
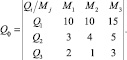
Численное значение в каждой таблице, то есть ее элемент qij, определяется двумя параметрами – индексами при Qi и Mi. Так, например, из первой таблицы q12 = 15, а из второй таблицы q22 = 4. Если количество индексов в строке таблицы или в столбце будет более десяти, то между индексами придется писать запятую. В общем виде, каждая из таблиц может быть представлена следующим образом (таблица товаров):
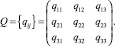
Таблица элементов qij, расписанных по m строкам и n столбцам, называется матрицей. Если число строк и столбцов совпадают (m = n), то матрица называется квадратной. Наибольшее число строк (или столбцов) в квадратной матрице определяют ее порядок.
Таблица товаров является, таким образом, квадратной матрицей третьего порядка (матрицей товаров). Рассмотрим действия (операции), которые можно производить с матрицами.
Имея матрицы закупок товаров за каждый месяц, легко подсчитать количество товаров, приобретенных за два месяца. Для этого, действуя по смыслу, необходимо сложить числа в соответствующих местах обеих матриц. В результате получаем общую матрицу закупок товаров.
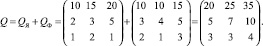
Таким образом, матрицы можно складывать по правилу:
.
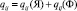Очевидно, что если матрицы закупок за каждый месяц одинаковы, то при поиске общего количества товаров за k месяцев, каждый элемент матрицы необходимо сложить k раз, то есть умножить на k. В общем виде это записывается следующим образом: Q = kQЯ. Поэтому матрицы можно умножать на число.
Пусть теперь нас интересуют ежедневные затраты, производимые за три дня покупок товаров трех сортов в трех различных магазинах, то есть, в общем случае, по разной цене. Теперь мы имеем две матрицы: матрицу закупок товаров Q = {qij} за три дня и матрицу цен P = {pij} товаров различного сорта в трех магазинах. Очевидно, что произведение количества товаров на соответствующие им цены, позволит определить произведенные затраты Y.
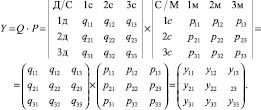
В таблицах закупок товара и цен использованы следующие обозначения: Д – дни; С – сорт товара; М – номер магазина. Теперь опишем матрицу Y = {yij}, которая получилась в результате предварительных расчетов. Для этого выберем произвольный элемент, например y23, и рассмотрим процедуру его вычисления. Индексы при элементе указывают, что речь идет о затратах второго дня при покупке товаров всех сортов в третьем по номеру магазине. Для того, чтобы получить соответствующее число, необходимо выбрать из матрицы товара за второй день товары первого сорта (q21) и умножить это количество на цену товаров первого сорта по ценам третьего магазина (p13). Затем сюда прибавить затраты на закупку во второй день товаров второго сорта (q22) по ценам третьего магазина (p23) и, наконец, сложить с затратами за второй день по закупке товаров третьего сорта (q23) по ценам третьего магазина (p33). В итоге имеем:
.
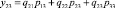Можно заметить, что при сложении, первый и последний индексы не изменяются, а суммирование производится по промежуточному индексу, стоящему между первым и последним. Поэтому для произвольного элемента матрицы затрат следует составить равенство:
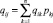
где n – порядок матрицы Y.
Таким образом, матрицы можно умножать и правилом умножения является полученное равенство. В матричной форме это можно записать так:
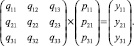
Рассмотрим, в качестве примера, систему линейных уравнений в виде: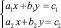 
, которую перепишем следующим образом:
,
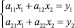где произведена замена: a1 = a11; b1 = b12; a2 = a21; b2 = b22; x = x1; y = x2; c1 = y1; c2 = y2. При этом смысл системы уравнений не изменился, а запись получила новую интерпретацию в матричной форме. Действительно, по правилу умножения матриц, будем иметь:
.
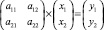Теперь очевидно, что записано равенство, в котором использованы квадратная матрица второго порядка A = {aij} и две матрицы – столбцы – для переменных (x1, x2) и (y1, y2). Первую из них обозначим X = {xi}, а вторую Y = {yi}. Тогда вместо системы уравнений, приведенной выше, будем иметь матричное уравнение: AX = Y.
Рассмотрим теперь применение матричного исчисления к задачам межотраслевого баланса в экономической сфере. Для простоты ограничимся анализом взаимодействия двух предприятий, принадлежащих различным отраслям производства товаров. Совокупный продукт, производимый каждым предприятием, можно разделить на три части, одна из которых идет на собственные нужды (πii), вторая – на обмен с предприятиями другой отрасли производства (πij) и, наконец, третья часть (yi) представляет собой объем продукции, идущей к потребителю. Каждая из этих частей имеет денежное выражение, поэтому все величины можно будет сравнивать без какого-либо переводного коэффициента. Система, состоящая из двух предприятий (также можно говорить и о двух отраслях) представлена на схеме (рис. 50). Обозначая совокупный продукт первого предприятия x1, а второго предприятия x2, получаем систему уравнений, верхнее из которых относится первому, а нижнее ко второму предприятию:
.
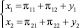На собственные нужды затрачивается доля a11 от совокупного продукта x1, равная π11/x1, то есть можно записать равенство: a11 = π11/x1.
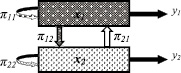
Рис. 50. К межотраслевому балансу двух предприятий
Соответственно, a12 = π12/x2, так как полученный вторым предприятием от первого предприятия поток промежуточного продукта π12 составит долю от совокупного продукта x2 второго предприятия.
Аналогично рассуждая, имеем: a22 = π22/x2, a21 = π21/x1. Поэтому систему уравнений можно переписать следующим образом:
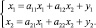
Полученная система уравнений, представляющая собой баланс предприятий, может быть записана в матричной форме:
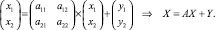(3.5.1)
Вектор X в этом уравнении представляет собой валовой продукт, вектор Y конечный продукт совместной деятельности предприятий, а матрица А является матрицей прямых затрат. Если в системе совместного выпуска продукции участвует много предприятий и целые отрасли, то векторы становятся многомерными, а матрица затрат имеет высокий порядок.
Матричная модель межотраслевого баланса была впервые предложена в экономике нобелевским лауреатом В. Леонтьевым и уравнение (3.5.1) называется уравнением Леонтьева. Рассмотрим пример на решение уравнения Леонтьева.
Допустим, что необходимо определить конечный продукт деятельности предприятий (или диктуемое спросом, предложение на рынке) Расчет производится при заданных условиями затратах и знании совокупного продукта предприятий, участвующих в совместной деятельности. Тогда, как это делается с обычными уравнениями, переносится в одну сторону «неизвестное», а в другую – «известное». Из уравнения Леонтьева, в этом случае, получим матричное уравнение: Y = X – AX, которое необходимо решить.
Для решения введем единичную матрицу I, то есть такую, произведение которой на любую матрицу A не меняет ее коэффициентов aij. Поэтому такая матрица и названа единичной, поскольку она, так же как обычная единица среди чисел, при умножении не меняет соответствующей величины. По определению единичной матрицы, можно записать, в частности, для матрицы Х следующее выражение: X = I∙X. Легко показать, что свойствами единичной матрицы обладает «диагональная» матрица, у которой все элементы с одинаковыми индексами (i = j) равны единице, а с различными индексами (i ≠ j) равны нулю. Действительно, 0. Тогда решаемое матричное уравнение можно записать сле- дующим образом:
Y = IX – AX = (I – A)X.
В скобках этого уравнения разность матриц, которая, как и сумма матриц, также является матрицей. Обозначим эту матрицу В. Тогда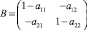 
и после вычисления соответствующих коэффициентов, по известной матрице А, можем найти матрицу Y, используя правило умножения матриц: Y = BX.