Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
§ 3.6. Модель экономической системы, основанной на связях
Рассмотренную модель Леонтьева легко обобщить на систему, образованную связями между предприятиями или финансовыми структурами. Пусть мы имеем фазовое пространство состояний эволюционирующей системы, для которой определены основные социально-экономические параметры выраженные в определенных единицах измерения. Пусть также в этом пространстве могут существовать элементарные производители, объединяющиеся между собой внутренними и внешними связями. Под словом «существовать» будем понимать «иметь определенные параметры». Наличие внутренней связи между элементарными производителями будет указывать на их объединение в одну подсистему, а наличие внешних связей будет характеризовать взаимодействие подсистем между собой (как в модели Леонтьева).
Для элементарной подсистемы количество внешних связей ограничено и возникает стремление к расширению, то есть к увеличению числа связей, путем их объединения в подсистему.
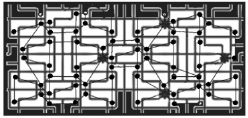
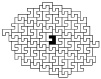
Рис. 51. Граф сети для разбиения пространства на области
Процесс «накопления» параметров в фазовом пространстве будет означать переход всей системы из условно выбранного начального состояния (с малыми параметрами) на новый уровень с другими параметрами.
Если параметры меняются дискретно, то совокупность большого числа переходов приведет фазовое пространство, в котором зафиксированы все этапы эволюции, к разбиению на отдельные, в общем случае, не элементарные области. Этот процесс назовем «кластеризацией». Условно выбранные точки – центры областей – задают математическую структуру сети, называемую графом (рис. 51).
Общие границы между отдельными подсистемами в разбиении выделяют «соседей» выбранной подсистемы, другими словами, количество внешних связей (ребер графа). Таким образом, результат развития системы, будет геометрически представлять собой своеобразную «карту местности», на которую наложен «растущий» из условно выбранной начальной области, граф.
Тем не менее, развитие системы, происходящее без разрыва связей должно выглядеть как переход от первого «окружения» исходной области ко второму окружению и т.д. с соблюдением принципа сохранения локальных (индивидуальных) правил соседства, основанных на связях. Исследование разбиений показало, что хаотически распределенные локальные связи между подсистемами не приводят к устойчивой динамике роста, пока в качестве согласования на связи не будет наложено условие симметрии. Учитывая важность периодических процессов в природе, выберем в качестве симметрического преобразования элементарные трансляции, образующие решетку так, как это принято в физике твердого тела. Для конечного числа подсистем это приводит к понятию фундаментальной области периодического разбиения, кластера, состоящего из ограниченного набора этих подсистем, трансляционно размноженных (перенесенных) в основных направлениях изменения параметров системы.
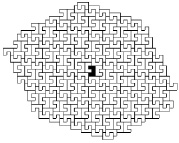
Процесс эволюции системы начинается с выбора исходной подсистемы, ее первого окружения ближайшими соседями, затем второго окружения и так далее, пока не начинает выявляться стационарная структура роста (рис. 52).
В частности, в нанотехнологии, отдельные структуры, составленные из молекул (атомов) способом «накопления массы», давно исследуются и называются «нанокластерами» (§1.12). Устойчивость нанокластеров достигается тогда, когда на каждом слое (или на поверхности сферы в трехмерном пространстве) создается плотная «упаковка», то есть построение слоя завершено. Количество молекул на завершенном слое называется «магическими числами» и они определяют устойчивость каждого кластера. Информация о структуре определяется по картине рассеяния волн на нанокластере (когда это возможно) и, при больших размерах, выстраивается в «обратную решетку». Эта решетка определяет многие свойства кластеров и теоретически рассчитывается с помощью математических методов, называемых преобразованиями Фурье. Справедливо и обратное, когда расчет с применением преобразования Фурье от обратной решетки определяет структуру самого кластера.
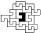
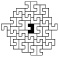
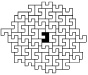
(1) (2) (3) (4)
(5) (6)
Рис. 52. Поэтапное развитие системы (1–5); стационарная структура (6)
Для периодических структур доказана теорема В. Журавлева об устойчивой форме послойного роста структур, определяющей форму кристалла в виде многогранника (многоугольника в двумерном случае). Из непериодических структур особый интерес представляют квазипериодические, которые можно рассматривать как модели квазикристаллов.
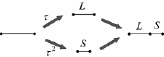
Рис. 53. Деление отрезка с использованием золотого сечения
Простейшим с точки зрения их устройства следует считать одномерные квазипериодические разбиения. Самым известным их них является так называемый одномерный кристалл Фибоначчи – одномерное квазипериодическое разбиение, построенное на основе золотого сечения. Золотым сечением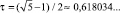 
называют один из корней квадратного уравнения x2 + x – 1 = 0. С помощью золотого сечения можно разбить произвольный единичный отрезок на два отрезка длиной τ и τ2 (рис. 53). Построим с помощью этого разбиения последовательность отрезков по следующей рекуррентной процедуре. В качестве начальной последовательности выберем один отрезок единичной длины. Каждую следующую последовательность будем получать из предыдущей последовательности разбиением всех единичных отрезков с последующим растяжением всей последовательности в 1/τ раз. Разбиение отрезков называют инфляцией, а последующее растяжение – дефляцией, поэтому сам метод называют методом инфляции-дефляции. На рис. 54 показаны первые 6 итераций построения последовательности отрезков.
Рис. 54. Первые шесть итераций построения последовательности отрезков
Заметим, во-первых, что каждая полученная последовательность отрезков содержит предыдущую как часть, во-вторых, количества коротких и длинных отрезков на k-м шаге соответствуют двум последовательным членам tk и tk+1 последовательности Фибоначчи (1, 1, 2, 3, 5, 8, …). Поэтому, если рассмотренную процедуру продолжить в бесконечность, в пределе получим бесконечное разбиение на отрезки двух типов, которое не может содержать параллельный перенос, так как в пределе отношение количеств отрезков разного типа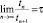 
– иррациональное число.
В двумерном случае аналогом одномерного квазикристалла Фибоначчи можно считать двумерное квазипериодическое разбиение Рози. Для его построения рассмотрим кубическое уравнение x3 + x2 + x – 1 = 0, которое имеет один действительный корень ς ≈ 0,543689... и два комплексных корня β ≈ –0,771844 – 1,115142i и комплексно сопряженный к нему. В качестве исходного элемента выберем фигуру T с фрактальными границами, которую называют фракталом Рози. Умножая множество точек на комплексной плоскости, принадлежащих T, на β–1, β–2 и β–3, получим фигуры TR, TG и TB, соответственно, которые разбивают исходную фигуру T на подобные ей фигуры (рис. 55).
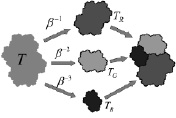
Рис. 55. Разбиение фрактала Рози на три подобные фигуры
Это разбиение задает инфляцию, а в качестве дефляции возьмем умножение на β. Если в качестве исходного элемента взять так называемое ядро – совокупность фигур TR, TG и TB вблизи начала координат, то, применяя инфляцию-дефляцию, получим последовательность конечных разбиений на плоскости, которая в пределе дает квазипериодическое разбиение всей плоскости, названое разбиением Рози. На рис. 56 представлены 5 первых итераций построения квазипериодического разбиения Рози.
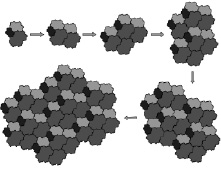
Рис. 56. Первых 5 итераций построения квазипериодического разбиения Рози
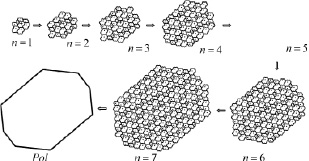
Рис. 57. Первые 7 координационных окружений и восьмиугольник роста разбиения Рози
Интересным представляется исследование послойного роста квазипериодического разбиения Рози. Выберем, для определенности, в качестве затравки послойного роста одну из фигур TR – фигуру первого типа. На рис. 57 показан процесс послойного роста и формирующийся при этом многоугольник послойного роста для разбиения Рози. Разбиение Рози имеет многоугольный рост в форме выпуклого центрально-симметричный восьмиугольника.
Для сложных экономических систем, связанных с финансовыми накоплениями, их состояние находит отражение в биржевых индикаторах, которые меняются так, что задача прогнозирования значительно отличается своей сложностью от задачи роста наноструктур, тем более, что и в этой области многие задачи еще не решены. Тем не менее, симметрия, как наиболее продуктивный метод анализа систем, регулирует все сферы научного подхода к любой системе и уже давно используется при анализе состояния рынка («волны Элиотта», то есть наличие периодичности или трансляционной симметрии; «числа Фибоначчи», определяемые вращательной симметрией оси пятого порядка, циклы Кузнеца и др.). Следует учесть, что при анализе симметрии экономических систем, так же как и при анализе структур вещества, существует большое разнообразие и в самих типах внутренних симметрий, поэтому получение информации в этой области требует индивидуального подхода к каждой задаче. При внедрении компьютерных методов математического моделирования самих систем и их свойств, то есть создании так называемых «торговых или биржевых роботов», ситуация может измениться в сторону увеличения вероятности прогнозирования, адекватного будущей реальности. В основу многих методов моделирования кладется модель разбиения пространства состояния системы на отдельные кластеры.