
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.6 Автоматизация анализа модели
Согласно синергетическим представлениям, для того чтобы система могла перейти в новое устойчивое состояние, необходимо текущее состояние сделать неустойчивым. Развитие любой сложной открытой системы всегда проходит через чередование стадий порядка и хаоса.
В этом случае благодаря явлению бифуркации у системы возникает выбор из нескольких устойчивых состояний, среди которых, возможно, находится и то, ради которого было оставлено предыдущее. Как известно, явление бифуркации соответствует нелинейному поведению системы, поскольку с математической точки зрения появление выбора из нескольких состояний означает, что уравнение, описывающее эволюцию системы, имеет несколько стационарных решений, т.е. является нелинейным.
Переход системы от одного устойчивого состояния к другому через неустойчивое и бифуркацию происходит в результате изменения интервала значений управляющих параметров - постоянных величин, входящих в эволюционное уравнение). С помощью управляющих параметров внешняя среда закрепляет свои отношения с системой.
Изменение управляющих параметров сказывается в первую очередь на изменении направления развития системы к тому или иному устойчивому состоянию – аттрактору (участку фазового пространства, окруженного областью притяжения, попав в которую, система в дальнейшем развивается только в направлении этого аттрактора).
Таким образом, в изменяющихся внешних условиях эволюция системы представляет собой последовательность различных аттракторов, переход между которыми происходит через неустойчивые состояния и бифуркации. Среди аттракторов названной последовательности могут быть, во-первых, нежелательные для системы, и, во-вторых, хаотические (странные), в которых процессы разрушения преобладают. Не попасть в область притяжения такого аттрактора или выйти из нее можно, изменив значения управляющих параметров. Поскольку не все постоянные (медленно меняющиеся с течением времени) параметры системы являются управляющими, поиск последних и определение интервалов их значений становится задачей синергетического исследования модели.
Система уравнений (2.16) – (2.18) по своей структуре подобна известной системе Лоренца, которая в общем случае не имеет аналитического решения. Было проведено численное исследование системы при различных значениях управляющих параметров.
В качестве бифуркационного параметра был выбран параметр l. В результате был найден ряд аттракторов типа "предельный цикл", различающихся своей конфигурацией: от простого предельного цикла (рис. 2.1, а) до предельных циклов со сложной конфигурацией (например, как на рис. 2.1, 6). Все эти состояния соответствуют устойчивому поведению фирмы, которое в зависимости от внешних условий приобретает ту или иную сложность.
Наличие аттрактора у исследуемой системы является следствием процесса самоорганизации: c течением времени все переменные системы “подстраиваются” под главные – параметры порядка, которые задают положение и форму аттрактора.
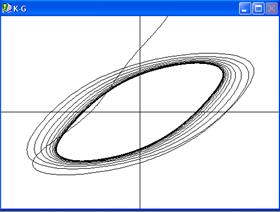
а) d =0,6; l =2,46

б) d =1; l =3,55
Рисунок 2.1 - Аттрактор системы (2.16) – (2.18) при a =5; g =1; m =2,1; b =8.Показана проекция на фазовую плоскость в безразмерных координатах K и G.
Также было найдено такое соотношение значений управляющих параметров, при котором фирма попадала в аттрактор, изображенный на рис. 2.2, а. Его фазовый портрет похож на фазовый портрет хаотического аттрактора Лоренца, что доказывает применение применили более точного критерия - показателей Ляпунова.
В трехмерной системе координат в случае хаотического аттрактора один показатель Ляпунова должен быть положительным, другой отрицательным, а третий равен нулю. В результате вычисления этих показателей для значений управляющих параметров, указанных под рис. 4.5, а, были получены следующие показатели Ляпунова: 0,22; 0,00; -3,22. Такое распределение знаков позволяет утверждать, что малое предприятие, основная деятельность которой определяется законом (2.16) – (2.18), имеет реальную возможность попасть в хаотический аттрактор Лоренца, если ее управляющие параметры примут соответствующие значения.
Исследование экономико-синергетической модели развития малого инно-вационного предприятия проведено в разработанной автоматизированной системе «Синергетический анализ развития малого предприятия».
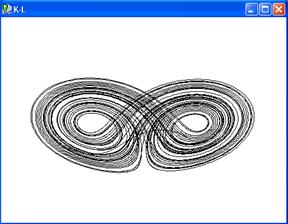

а) g =1
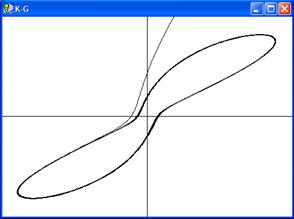
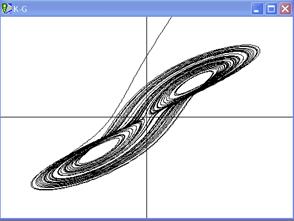
б) g=2
Рисунок 2.2 - Аттрактор системы (2.16) – (2.18) при a =5;; m =2,1; b =8;d =1; l =4,1. Показана проекция на фазовую плоскость в безразмерныхкоординатах K –L и K – G .
Для подтверждения достоверности результатов, полученных с помощью разработанной автоматизированной системы, было проведено исследование экономико-синергетической модели на системе Dynamics Solver, v. 1.56.2 (автор J.M. Aguirregabiria).
В результате анализа модели развития предприятия малого бизнеса было показано, что при определенном соотношении управляющих параметров появляются устойчивые предельные циклы, а также возникает опасность оказаться в хаотическом аттракторе Лоренца, который возникал лишь при определенном соотношении управляющих параметров. Следовательно, изменив значения некоторых из них, можно избежать области притяжения нежелательного аттрактора.
