
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.3.4. Определение продолжительности ψ1 при (+ρ min)
При известных кривизне краев детали (ρ) и соотношениях скоростей инструментов, а также с учётом ошибки подачи детали в начале процесса условия работы машины определяются как:
ψ1 > ψ2.
Из рис. 3.8 имеем: где
В2В/О2В = sinψ2/2; sinψ2/2 = Su/2(ρ – ℓ);
В2∙В/Р1В2; Su/2(Р1В2) = sinψ1/2;
тогда Su/2(Р1В2) > Su/2(ρ – ℓ) или ρ1В2 < (ρ – ℓ).
Откуда
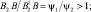
ψ2/2 = arcsin Su/2(ρ – ℓ);
ψ2 = 2arcsinSu /2(ρ – ℓ).
Тогда
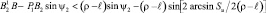
или
ψ1 = –А1 (1 – К1)/(К2 – К1)∙(cosφ2 – cosφ1) >
> [Su arcsin Su/2(ρ – ℓ)] / (ρ – ℓ) sin [2arcsin Su/2(ρ – ℓ)]. (3.5)
Если начало прокола и перемещение иглы соответствует началу вращения ведущего вала, то φ1 = 0. Тогда угол поворота ведущего вала, соответствующий концу свободного вращения детали до упора, определяется по формуле:
φ2 > arccos{[Su arcsin Su/2(ρ – ℓ)]/(ρ – ℓ)sin[2arcsin Su/2(ρ – ℓ)]×
×[–А1 (1 – К1)/(К2 – К1)]}. (3.6)
Как видно из выражения (3.6) угол φ2 зависит от величины Su и ρ, а также от соотношения скоростей инструментов VВ/VС и расположения упора. Так, с увеличением ρ и соотношения скоростей инструментов продолжительность поворота ведущего вала φ2 машины, обеспечивающая контакт края детали с упором уменьшится.
Далее определены ρmin в конце свободного поворота детали с применением ФТОУ и получены аналитические зависимости, определяющие взаимосвязь между поворотом детали инструментами ФТОУ и кривизной контура детали, а также кривизна контура детали описаны через возможный угол поворота детали с помощью ФТОУ. Кроме того, установлена зависимость влияния расположения упора на угол поворота ψ1.
