Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Баубеков С. Д., Таукебаева К. С.,
3.3.6. Определение ускорения детали при ее ориентации с применением ФТОУ
Для решения динамических вопросов процесса ориентирования необходимо иметь аналитические зависимости, определяющие ускорения детали. Выше определены общий угол ориентации детали в одном цикле ориентирования ее с помощью ФТОУ.
Отмечено, что ψ1 > ψ2, то есть на первом этапе угловая скорость детали больше чем на втором. Поэтому определяем скорость центра масс детали Vs в точке S именно на этом этапе – 01 (рис. 3.9) [20, 27, 29,30]
ω1 = (VB – VC)/b.
Тогда
VS = ω1 p S;
где p, S – расстояние от полюса p1 до центра тяжести детали. Центр тяжести детали имеет координаты S(Хs, Ys) (рис. 3.9). При перемещении детали относительно полюса изменяется угол æ между неподвижной ХОY и подвижной системой координат Х1О1Y1, т.е. æ(t), а следовательно изменяются и координаты (t) и Ys точки S в основной системе отсчёта
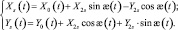(3.9)
rs = ro1 – ρ, (3.10)
где координаты Х0 и Y0 – постоянные величины, а также угол æ определены.
Продифференцировав по времени Х2s и Y2s, найдём проекции точки s на координатные оси:
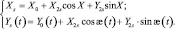(3.11)
Эту же зависимость можно получить продифференцировав по времени (3.10):
drs/dt = dro1/dt – dρ/dt. (3.12)
Заметим, что
drs/dt = Vs; dr01/dt = V01; dρ/dt = Vs01,
скорость точки S относительно подвижной системы координат О1Х1Y1 представляет вращение тела вокруг оси О1Z1, направленной перпендикулярно плоскости чертежа (см. рис. 3.9)
V0s = ω01∙ρ1, (3.13)
где ω01 – угловая скорость вращения детали вокруг точки О1.
Vs = V01 – ω01∙ρ1 = V01 – V0s. (3.14)
Таким образом, скорость центра тяжести равна геометрической сумме скорости полюса и скорости точки S при вращении её вокруг МЦВ, совпадающего с пoлюсом О1. Как видно, угловая скорость вращения детали не зависит от выбора пoлюса, поэтому ω01 = ω1.
Тогда
Vs = V01 – ω01∙ρ1,
где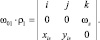 
(3.15)
Здесь ωz = ǽ; Х1s = Хs sin æ – Ys cos æ,
Y1s = Хs cos æ – Ys sin æ.
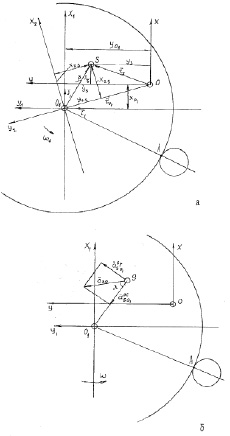
Рис. 3.9. Определение ускорения детали при ее ориентации
Модуль Vo1s = ω1O1s, так как ωz = ǽ, то при ω1 > O, вращение происходит против часовой стрелки.
Из (3.11) после проектирования на оси координат можно получить при æ = Ψ1.
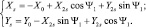(3.16)
Определение ускорения центра масс ориентируемой детали
Для этого продифференцируем равенство (3.16) или выражение (3.14) по времени
dVs/dt = dVO1/dt – (dω/dt∙ρ + dρ/dt). (3.17)
Здесь dVs/dt = аs; dVO1/dt = ao1; dρ/dt = ω∙ρ = VO1S; dω1/dt = ε1 – вектор углового ускорения; ε1 – направлен перпендикулярно плоскости чертежа и определяется по формуле
ε1 = d/dt (Ψ1k) = (Ψ1k).
Таким образом, ускорения точек О1 и S связаны между собой соотношением
as = ao1 = (ε1∙ρ1 + ω1∙VO1S). (3.18)
Два последних слагаемых в (3.18) определяют ускорение точки S при закрепленной точке О1 (ао1 = о). Поэтому их сумма
(ε1∙ρ + ω1∙VO1S) = ao1s,
дает ускорение точки S во вращательном движении относительно системы О1Х1Y1, а направление ao1s совпадает с направлением прямой, соединяющей точку S с полюсом О1, ω1∙VO1S; a ε1∙ρ1 перпендикулярна SO1.
Итак, центростремительное ускорение точки S определяется как
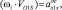
а вращательное ускорение этой точки определяется по формуле
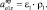
Модули этих составляющих будут
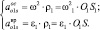(3.19)
Итак,
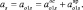(3.20)
Ускорение центра масс детали, приложенное в т. S, определяется как геометрическая сумма ускорения полюса, центростремительного и вращательного ускорений во вращательном движении детали относительно МЦВ (P1).
Из (3.20) определим угол, составленный вектором ao1s с направлением на полюс (рис. 3.7):
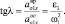
Отсюда видно, что угол λ не зависит от выбора полюса и во всех случаях при фиксированном времени одинаков. Модуль ускорения т. S при вращении детали вокруг МЦВ (Р1) также находится из (3.20):
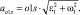
он зависит от расстояния точки S до О1. При совпадении мгновенного центра ускорения (МЦУ) с полюсом О1:
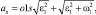(3.21)
где ω1 = (Vв – Vс)/b.
Модуль углового ускорения определяется из формулы:
ε1 = dω1/dt = d2Ψ1/dt2, (3.22)
где из (3.6) напишем значение
Итак, подставляя (3.22) в (3.20) определим величину as.
Или после дифференцирования выражения (3.17) по времени получим ускорения aхs и aуs, а полное ускорение точки s получим:
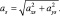(3.23)
Ускорение во втором этапе перемещения детали определяется аналогично. При этом:
as2 < as1. (3.24)
Из вышеизложенного следует, что скорость и ускорение центра масс детали определяются в основном положением МЦВ, величиной угловых скоростей и ускорений детали, а также соотношением скорости рабочих инструментов машин. Заметим, что при свободном вращении эти величины (Vs и as) не зависят от кривизны краёв, а во многом определяются расположением упора. При перемещении детали после контакта её края с упором эти величины в основном определяются кривизной краёв детали и расположением упора, причём вогнутые края имеют при свободном перемещении минимальную величину Vs и as, по сравнению выпуклыми краями.
Следующий вопрос, касающийся технологической возможности СМК, предварительное ориентирование детали относительно рабочего органа ФТОУ перед шитьем. Поскольку данный способ используется для выполнения швейной строчки, а эквидистантность строчки краю детали имеет важное значение, требуется определить кинематическую составляющую ошибки позиционирования детали.