Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Баубеков С. Д., Таукебаева К. С.,
3.5.3. Метрический синтез вновь созданного механизма отклонения иглы ФТОУ-2
Целью исследования является определение скорости перемещения иглы как функции угла поворота главного вала машины [27]. В этой работе дана методика проведения метрического синтеза отклоняющей иглы, предложенного ФТОУ. Воспользуемся методикой этого исследования для определения кинематических характеристик ФТОУ-2 типа «рейка-рейка + отклоняющая игла», дополняя их новыми исследованиями на ЭВМ [20, 29, 30, 33].
Допустим, что положение точки D обеспечивает величину отклонения иглы (SH = 2 мм). В созданном ФТОУ-2 эта величина устанавливается автономно, т.е. независимо от перемещения рейек (также как и в ФТОУ-1).
Для выполнения кинематического анализа разделим вновь созданный механизм, приведенный на рис. 3.11, на следующие группы: ABCDA, DCGQD и QMK (рис. 3.12). Рассмотрим условия работоспособности каждой группы и составим уравнения условия замкнутости. В результате математической обработки определим длину базового вектора, углы, определяющие положения каждого звена, угловые скорости звеньев,
передаточные отношения звеньев. Дифференцируя их по обобщенной координате, получим систему линейных уравнений, для решения которых воспользуемся формулой Крамера. Определим угловые ускорения каждого звена. Имея плечо отклоняющей рамы иглы, определим величину горизонтального отклонения иглы как функцию поворота главного вала.
Ниже, опуская подробности методики метрического синтеза, приводим основные его результаты [20].
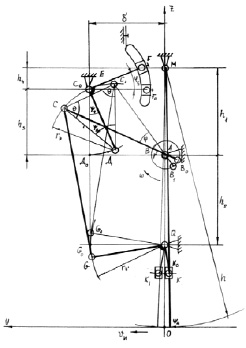
Рис. 3.11. К синтезу модернизированного механизма отклонения иглы 330 кл.
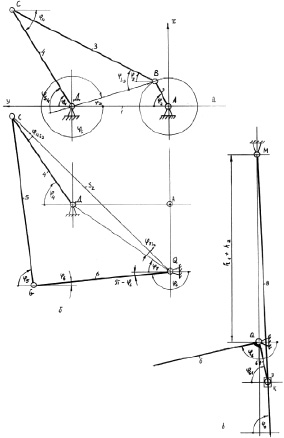
Рис. 3.12. К метрическому синтезу модернизированного механизма иглы
Для определения угловых ускорений звеньев и соответствующих передаточных отношений запишем следующее уравнение [20]:
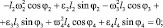
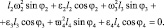(3.33)
Система является линейной относительно искомых величин ε3 и ε4. Систему (3.33) иногда преобразуют относительно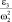 
и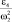 
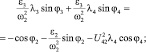
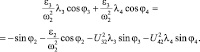(3.34)
Корни выражения (3.33) находят по формуле Крамера.
Итак, аналогично определяем передаточные отношения для других звеньев (см. рис. 3.12 запишем следующее уравнение):
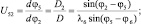
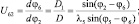
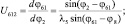
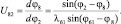(3.35)
Определение угловых скоростей звеньев:
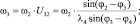
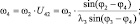
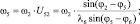
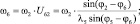
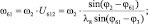
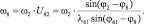(3.36)
Определение скорости перемещения иглы. Используем выражение (см. рис. 3.11)
νВ = ω8∙h,
где h – длина звена 8; ω8 – угловая скорость звена 8.
Подставляя значение угловой скорости ω8 получим:
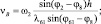
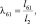
где l2 и l61 длины звеньев 2 и 61; ω2 – угловая скорость звена 2; φ2, φ61 и φ8 углы поворотов звеньев 1, 6 и 8. Здесь φ2 – берется из разд. 3.1.4 формула (3.6)
Обозначив
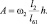
Запишем
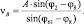(3.37)
Полученное выражение (3.37) использовано при определении условия работоспособности ФТОУ-2 и ФТОУ-3 (см. разделы 3.5.3, 3.8). Разработана программа для кинематического исследования вновь созданного механизма отклонения иглы, после обработки результатов исследования на ЭВМ проведен уточненный расчет кинематических характеристик ФТОУ. Полученные оптимальные параметры механизма были использованы при разработке ФТОУ для модернизации ряда машин 430, 597,697 кл. [30, 34, 38, 49, 51, 55].