Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Баубеков С. Д., Таукебаева К. С.,
3.6.2. Исследование процесса ориентации детали при наличии сухого трения
В работах [20, 29] исследовано взаимодействие тела с плоскостью во время его перемещения, где отмечено, что прилагаемая сила на тело тратиться сначала для приодолевания силы трения между телом и плоскостью. Только после этого эта сила перемещает тело, причем, тело перемещается скачкообразно. Это объясняется наличием между телом и поверхностью, по которой перемещается тело, сухого трения.
Влияние сухого трения на процесс ориентированного перемещения детали по плоскости с применением ФТОУ не изучено. Поэтому этот вопрос на наш взгляд, представляет научно-практический интерес.
Предположим, что давление детали (в нашем случае, рис. 3.18) на поверхность игольной пластины швейной машины в каждой точке пропорционально ее локальной плотности р (отнесенной к площади детали) 20, 36]. Это означает, что вертикальные сдвиговые напряжения в детали пренебрежимо малы.
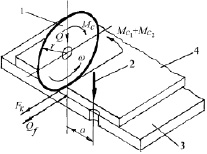
Рис. 3.18. К определению Мс:1 – ролик транспортирующий; 2 – игла; 3 – игольная пластина; 4 – деталь
Обозначим через V, R вектор скорости центра масс и радиус вектор, ω – угловая скорость, k – коэффициент трения детали по плоскому основанию, m –масса детали, I – центральный момент инерции относительно вертикальной оси, g – ускорение силы тяжести, как это указано в приведенных работах.
Составим уравнение движения детали, для чего используем методику из [20]. Сила сухого трения dF, действующая на элементарной площадке ds поверхности игольной пластины, пропорциональна давлению р и направлена против вектора скорости V элемента, то есть, при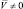 
:
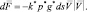(3.44)
Здесь предполагается, что сила трения, действующая на неподвижный элемент детали при 
отсутствует. Такое предположение определено для детали, не имеющей сосредоточенную массу.
Введем систему координат, связанную с деталью, начало координат в центре масс детали.
Обозначим через 
– радиус вектор, соединяющий начало системы и элемент ds поверхности игольной пластины. Скорость элемента ds равна
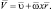
Главный вектор F и главный момент М относительно центра масс равны [20]:
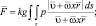(3.45)
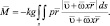(3.46)
В координатной форме (3.45) и (3.46) представим так [20]:
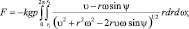
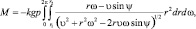
тогда масса и сила инерции детали определяется как:
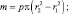
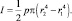(3.47)
С учетом сухого трения (рис. 3.18), а в нашем случае:
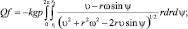(3.48)
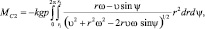(3.49)
где Mc1 = 0, т.к. в механизме отсутствует скольжение со стороны заготовки; Q = Nc – сила давления ролика на деталь; k = f – коэффициент трения детали об игольную пластину; r – расстояние от точки контакта инструмента до центра вращения (радиус ролика); Ψ – угол ориентирующего поворота детали в процессе шитья; υ – скорость детали; ω – угловая скорость детали; g – ускорение силы тяжести детали; Мс2 – момент сопротивления развороту вследствие защемления (материала) детали.
Тогда с учетом сухого трения, Fc1 запишем в виде:
Fc1 = Nc∙f1 + Qf,
где Q = Nc или
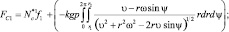(3.50)
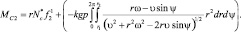(3.51)
Моменты сопротивления перемещению деталей роликами с учетом формулы из [30] будут:
M1c = F1c∙r1;
M2c = F2c∙r2.
Подставляя (3.48), (3.49) в (3.50), (3.51) определяем
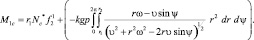(3.52)
Используя (3.50), (3.52) получаем формулу для определения параметров ФТОУ. Решая оптимизационную задачу определим необходимые значения величин: с1, с2, ∆пр1, ∆пр2, r1, r2, f1, f2.
В работе [30] приведены аналитические зависимости для определения реакции Ra, реакции отклоняющей иглы RB, и h1, h2.
Однако, надо отметить, что в приведенной работе влияние на процесс сухого трения не учтены.
Согласно рис. 3.19, б, определим плечи реакции
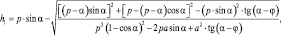(3.53)
где а – расстояние от края детали до середины иглы, что соответствует эквидистантности строчки относительно края детали (рис. 28, б); α – угол, определяющий расположение упора относительно ориентирующих инструментов (С – ролики, В – игла); φ – угол трения края детали об упор А(sinφ = Fa/Ra); ρ – величина кривизны края детали.
А другое плечо определяется как
h2 = bcos φ1, (3.54)
где b – расстояние между инструментами В и С;
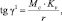(3.55)
где Мс – момент сопротивления перемещению деталей роликами; Kv – коэффициент буксования роликов (Kv = 0,82–0,92) [44]; r – радиусы роликов.
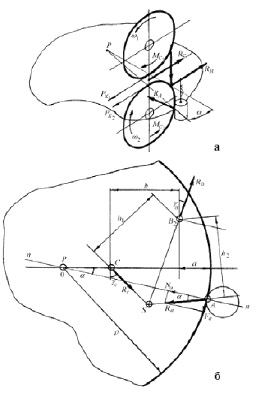
Рис. 3.19. а – схема взаимодействия ФТОУ с материалом; б – расчетная схема
Подставляя (3.54) в (3.55) получим:
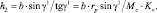(3.56)
Подставляя в (3.56) значения (3.53), (3.54) с учетом сухого трения имеем:
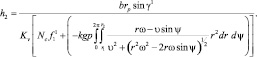(3.57)
где υ – скорость детали при ее ориентации; ω – угловая скорость детали при ее ориентации, а угол ψ принимается из раздела 3.3.2, cчитая, что рассматривается этап, соответствующий ориентации детали после соприкосновения ее края с упором, т.е. середине ориентации. Используя (3.57) и (3.53), определяем величины h2, h1 с учетом сухого трения.