Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Баубеков С. Д., Таукебаева К. С.,
3.6.3. Определение ориентирующей реакции ФТОУ с учетом сухого трения
Выше определены ориентирующие силы всех инструментов, участвующих в процессе ориентации детали относительно направляющего упора.
Рассмотрим влияние ориентирующей реакции (Rор) на деформацию края детали (рис. 3.20).
Реакция сил, действующих относительно нормали n-n в точке А (см. рис. 19) определяется по формуле
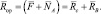(3.58)
Тогда деформация края детали при автоматической ориентации с применением ФТОУ, не должна превышать допускаемую величину [έ], то есть обеспечивается условие эквидистантности строчки относительно контура детали [30]
∆ < [έ], (3.59)
где έ – допускаемая деформация края детали упором.
Итак, для определения Na с учетом сухого трения и условия (3.59). Из принципа Д′Аламбера, запишем уравнение равновесия действующих сил:
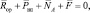(3.60)
где F – главный вектор относительно центра масс сил трения с учетом сухого трения; Pин – сила инерции перемещающейся детали, Pин = m∂a∂, где m∂ – масса, a∂ – ускорение детали; Na – нормальное давление детали на упор; Na = Racosφ; Rop – ориентирующая сила, определяется из (3.58).
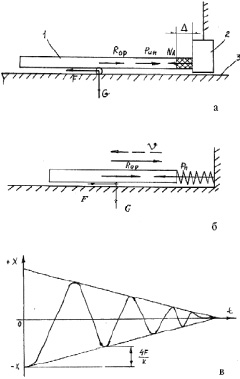
Рис. 3.20. Расчетная схема к определению Rор и амплитуды автоколебания
Из условия (3.59) запишем:
∆ = Na/с∂ < [έ], (3.61)
где с∂ – жесткость материала деталей, тогда с учетом (3.61) имеем
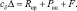(3.62)
С учетом того, что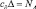 
, здесь
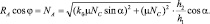(3.63)
А кулоновая сила сопротивления между материалом и поверхностью платформы машины
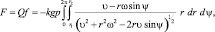(3.64)
где k = μ, а сила инерции определяется как Pин = ma, где ускорения центра масс детали, определены в главе 3.
Без учета Pин составим уравнения равновесия системы.
Подставляя в (3.58) значении (3.63) и (3.64) имеем
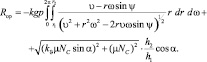(3.65)
Как видно, из (3.65) ориентирующая реакция зависит от влияния сухого трения и реакции упора Rа на край детали, что учитываем при дальнейшем исследовании «автоколебаний» детали при ее ориентации.
Итак, для определения «смятия» – деформацию края ограничительным упором, определим из условия (3.61) с использованием формул (3.63), (3.64):
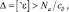
где из (3.64) и с учетом Pин:
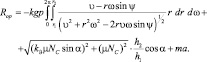(3.66)