Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Баубеков С. Д., Таукебаева К. С.,
3.7.1. Анализ работы механизмов ориентации и перемещения сшивающих деталей фрикционно действующими инструментами – ФТОУ-2
А. Механизм типа «тормозок-рейка»
В некоторых машинах, предназначенных для обработки деталей по краю, ориентация и перемещения деталей осуществляется с помощью рейки, тормозка и упора [30, 38, 49]. Здесь тормозок не способствует к перемещению материала, а препятствует ему. Тем самым мешает процессу ориентации детали при контурной обработке. Поэтому при изменении модуля кривизны контура детали их применение не приводит к успеху.
Для определения технологической возможности вновь предлагаемого способа и реализующих его устройств [30, 33, 42, 47], а также для сравнения их преимуществ перед известными устройствами, приводим результаты исследования системы «рейка-рейка».
Скорости и ускорения (J и а) движения таких деталей и силы их взаимодействия с рабочими инструментами зависят от многих факторов, определить влияние которых достаточно сложно, т.к. известными являются только направление скорости точки контакта края деталей о тормозок или об упор и величина силы прижатия деталей к рейке или ролику. Решение этой задачи можно выполнить в несколько этапов. Сначала следует определить скорость (J) движения деталей и силы их взаимодействия с рабочими инструментами без учета сил и моментов сил инерции. После этого можно определить ускорения (а) движения деталей, их инерционные нагрузки и повторно определить скорости движения деталей и приложенные к ним силы; причем при расчете можно учесть и деформации деталей. Дальнейших уточнений в большинстве случаев не требуется.
Ниже, изложено решение без учета сил инерции, деформации деталей при постоянных по величине силах, их взаимодействия с упором или тормозком и рейкой или роликами. Допустим, деталь (рис. 3.23, а) вращается вокруг МЦВ (Р), на нее действуют силы со стороны упора А, тормозка С и рейки В. Рассмотрим их взаимосвязь.
1. Определим γВ и γС, (рис. 3.23, б):
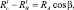(3.67)
где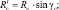 
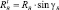, а величина RА определяется из условия SМВ = 0;
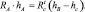
Тогда
RA = (hB – hc)/hA Rcsingc
и подставляя (3.67)
Rc(1 – (hB – hc)/hA∙cosb)∙singc = RB∙singB,
т.к. hA = hB∙cosb, то выражение
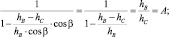
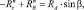(3.68)
где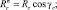 
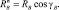
Величину RA окружности из условия SМс = 0.
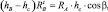
откуда
RA = hB – hc/hccosb∙RBsingc. (3.69)
И
cosgC = (cosgC – (hB – hC)∙sinb/hC∙cosb∙singB)∙RB/RC. (3.70)
Возведя в квадрат (3.68) и (3.69) и сложив их имеем:
А2(RB/RC)2sin2gB + (cos2gB – 2BcosgB∙singB + B2sin2gB) = 1.
Учитывая, что: sin2gB = 1/2 – 1/2∙cos2gB;
cos2gB = 1/2 + 1/2∙sin2gB
и что 2В∙cosgB∙singB = Bsin2gB; получаем:
A2/2(1 – cos2gB) + 1/2[(1 + cosgB) + B2(1 – cos2gB) – Bsin2gB] = (RC/RB)2.
Умножим левую и правую часть и уравненя на два и упростим равенство, тогда:
(–A2 + 1 – B2)cos2gB – 2Bsin2gB = 2(RC/RB)2 – A2 – 1 – B2,
обозначим:
–A2 + 1 – B2 = Csind;
2B = Ccosd;
2(RC/RB)2 – A2 – 1 – B2 = Д.
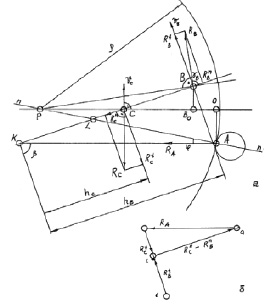
Рис. 3.23. Кинематический анализ ФТОУ-2
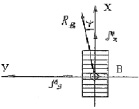
Рис. 3.24. К силовому анализу ФТОУ-2
Тогда
Csin(–2gB + d) = Д, (3.71)
где С = [(1 – A2 – B2)2 + 4B2]1/2;
tgd = 1 – A2 – B2/2B. (3.72)
По (3.71) и (3.72) определить gВ.
–2gB + 8 = arcsinД/С,
с учетом (3.70) получим
gB = 1/2(arctg∙1 – A2 – B2/2B – arcsinД/С). (3.73)
По (3.69) определим:
RA = hB – hC/hccosb∙RB∙singB (RB – считается известным)
2. Определим NB (рис. 3.24)
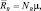
т.к. RB вектор, следовательно NB или m – векторы, по направлению совпадающие с RB.
В первом случае:
NB = NBX + NBY,
где NBX и NBY – проекция NИ по осям X и Y, величина их определяется
NBX = NB∙cosy;
NBY = NB∙siny.
Тогда
RBX = NBXmX = NBmXcosy;
RBY = NBYmY = NBmYcosy.
Следовательно
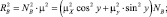
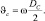
т.к. NB = RB/m; (mX = 0,4; mY = 0,3) то NB(2,5...3,3)RB.
Для анализа работы такого механизма была составлена блок-схема и программа на языке БЕЙСИК.
В этой программе анализируются зависимости gВ от RC/RB и RA от
RC/RB. Отношение RC/RB меняется в зависимости от mс и mВ, а также изменением NB и NC.
3. Определим RC/RB.
RB = NB∙mB и RC = NC∙mC, RC/RA = NC∙mC/NB∙mB.
(RC/RB)max = (NC/NB)max∙(mC/mB)max,
т.к. здесь N меняется с изменением толщины деталей в пределах ±5 %; m = 0,3...0,4, то
(RС/RВ)max = 1,05/0,95∙0,4/0,3 = 1,46;
(RС/RВ)min = 0,95/1,05∙0,4/0,3 = 0,685.
4. Определим hB, hC и β
Эти величины зависят от геометрических размеров рабочих инструментов, радиуса кривизны детали (от начала или конца транспортировки I и II положения механизма).
Найдем hB, hC и b для II положения (рис. 3.25).
Из DОРА:
ОРА = arcsin(AO/PA),
где OA – расстояние от оси детали до упора; r = РА – расстояние от МЦВ до упора.
Из DСВВ0:
СВ = [(СВ0)2 + (В0В)2]1/2,
где В0В – расстояние между вторым положением точки В и средним положением; В0В = S/2; S – длина стежка.
Из DСВВ0
ВСВ0 = arccos(B0С/СB).
Рассмотрим DKLA и СPL
Из DPLС следует что:
PLС = p – CРА – PСL,
т.к. углы PСL и BСB0 вертикальные, то они равны, следовательно
РLС = p – СPA – BСB0.
Из DKLA:
LKA = p – KLA – LAK,
где KLA – вертикальный угол, с учетом PLС; LAK – угол трения (с обозначением его j).
Тогда
LKA = p – (p – СPA – BСB0) – j
или LKA = СPA + BСB0 – j,
так как
b = p/2 – LKA, то b = p/2 – j – Q – G, (3.74)
где Q – угол ВСВ0; G – угол СВА.
Из DСОА найдем СА
СА = [(СО)2 + (АО)2]1/2,
где СО = СВ0 + B0O.
Тогда из СКА найдем КС = hc (по теорий синусов).
hC/sin(CAK) = CA/sin(p/2 – b), (3.75)
где CAK = arccos (CO/CA) + j – CPA.
Найдем hB,
hB = hC + CB. (3.76)
Выпишем отдельно (3.74), (3.75), (3.76), в том виде, в котором они записаны в программе
b = U + Д – Q – G, (3.76a)
где U – угол p/2; Д – угол j; Q = arccos(B0C/CB),
G = arcsin(AO/ρ);
hC = sinA1∙CA/sin(U – B1), (3.77)
где A1 – угол САК; В1 – угол b;
hB = hC + T; (3.78)
T = СB = [(СB0)2 + (S/2)2]1/2.
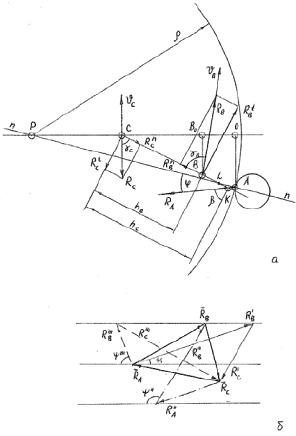
Рис. 3.25. К силовому анализу ФТОУ-2 («выпуклый контур»)
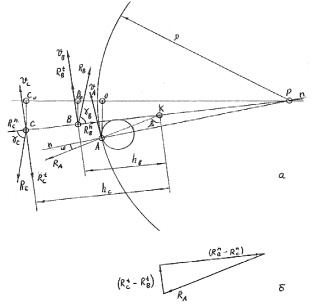
Рис. 3.26. К силовому анализу(«вогнутый контур»)
5. Найдем hB, hC и β для I положения (рис. 3.25, а).
(Рассчетная схема аналогична II положению)
Угол b определяется аналогично и он равен
b = U – Д + Q – G;
где U, Д, Q и G – определены выше.
hC = sinA1∙CA/sin(U – B1).
В результате анализа проведенного на ЭВМ получены следующие результаты и на основании, которых построены графики.
6. Определение области допустимого изменении угла γВ, то есть ту область, при которой механизм работоспособен (рис. 3.25,б)
Реакция RC всегда направлена вниз, иначе бы механизм был бы неработоспособен, следовательно, т.к.
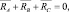(3.79)
то как видно из рис. 3.25, б, угол y может лежать в диапазоне 0 ≤ y ≤ p. Следовательно, если рассмотреть изменения угла b, то
gВ = y – (В0сВ), (3.80)
где В0сВ – угол Q, тогда
В0сВ = arccosB0c/cB = 0,46 рад,
для параметров по которым считают программу т.е.:
В0с = 4 мм, В0В = 2 мм.
Следовательно gВ = –0,46... +2,68 рад.
При «вогнутом» контуре все определяется аналогично.
7. Анализ полученных результатов
На рис. 3.27 построен график зависимости RA(RC/RB).
RA – основная реакция – определяет деформацию края детали, а следовательно, работоспособность устройства обработки деталей по краю. Из графика видно, что RA изменяется в довольно широких пределах: (0...5 Н). Для первого и второго положения дополнительной рейки значения (RA) различны.
На рис. 3.28 построен график зависимости RA(r). При обработке детали с радиусом кривизны r = 0–40 мм, RA изменяется в широком диапазоне и разница между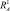 
и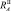 
значительна. При r > 40 мм, RA стабильна.
На рис. 3.29 построен график зависимости gВ(RC/RB).
Угол gВ определяется направлением RB и находится в пределах – 0,46 < gB < 2,68 рад.
В процессе работы машины этот угол изменяется в широком диапазоне 0,25 < g < 0,45 рад, причем, с увеличением RC/RB угол gВ уменьшается.
На рис. 3.30 приведен график зависимости RA(AO) – места расположения упора. С увеличением расстояния АО RA увеличивается.
Из анализа следует, что:
– направление RB и RC, а следовательно углы gВ, gС зависят от расположения рабочих органов, длины стежка (S), r, места расположения упора (ОА);
– в процессе работы машины они могут изменятся в широком диапазоне, вследствие изменения положения точки В относительно точек А и С, изменения величин mС, mВ, NC, NB и из-за различной толщины;
– различной плотности детали, а также различной деформацией его упором, может меняться и направление RA;
– поэтому ожидать устойчивых результатов работы таких механизмов(типа «тормозок-рейка») не следует.
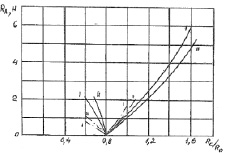
Рис. 3.27. К силовому анализу ФТОУ-2:
I – для первого положения дополнительной рейки;
II – для второго положения дополнительной рейки;
– для системы «тормозок – рейка»; – для системы «рейка – рейка»
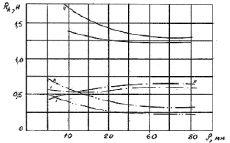
Рис. 3.28. К силовому анализу ФТОУ-2:
– для системы «тормозок – рейка»;
– для системы «рейка – рейка» – «выпуклый контур»
– для системы «рейка – рейка» – «вогнутый контур»
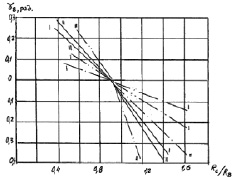
Рис. 3.29. К силовому анализу ФТОУ-2:
– для системы «тормозок-рейка»;
– для системы «рейка-рейка» – «выпуклый контур»;
– для системы «рейка-рейка» – «вогнутый контур»
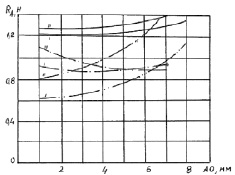
Рис. 3.30. К силовому анализу ФТОУ-2:
– для системы «тормозок-рейка»;
– для системы «рейка-рейка» – «выпуклый контур»;
– для системы «рейка-рейка» – «вогнутый контур»
Б. Синтез механизма типа «рейка-рейка» ФТОУ-2
В разрабатываемом механизме ФТОУ-2, предназначенном для обработки детали по краю, процесс ориентации и перемещения детали, осуществляется с помощью основной рейки, дополнительной рейки и упора. Причем, перемещения дополнительной рейки дифференцированно и зависит от кривизны детали.
Проанализируем работу такого механизма, т.к. перемещение дополнительной рейки зависит от кривизны контура детали, то рассмотрим возможности обработки вогнутого контура (выпуклого тоже).
1. Рассмотрим выпуклый контур т.к. расчетная схема аналогична (рис. 3.25), то определение γВ, RA, будет аналогичным.
В результате мы получим:
g = 1/2(arctg∙l – A2 – B2/2B – arcsinД/С),
где В = hB – hC/hc∙tgB;
А = hB/hC; C = [(1 – A2 – B2)2 + 4B2]1/2;
Д = 2(RC/RB)2 – A2 – 1 – B2,
т.к. дополнительная рейка подпружинена, то можно считать, что RC = const, следовательно, отношение RC/RB меняется в меньшем диапазоне:
(RC/RB)max = NCmC/NBmB = 1,0∙0,35/0,95∙0,3 = 1,22;
(RC/RB)min = NCmC/NBmB = 1,0∙0,35/1,05∙0,3 = 0,84.
Определение hC, hB и b для II – положения механизма (рис. 35) из DРОА
РВ0 = РО – В0О = РАcosOPA – B0O;
OPA = Q; a = arcsin(AO/PA).
То РВ0 = rсоsQ – B0O.
Из DPBB0 найдем угол ВРВ0 = G
G = BPB0 = arctgB0B/PB0; B0B = S/2;
G = arctg(S/2PB0).
Угол СРА с углом ВРА
СРА = p – ВРА = –Q – G + G.
Из DКРА найдем РКА
РКА = p – КРА – РАК = p – (p – Q – G) – j = –j + Q + G.
Тогда b = p/2 – РКА = p/2 + j – Q – G.
Из DРКА найдем РК по теореме синусов
РК = РА∙sinj/sin(p/2 – b);
PK = rsin(j)/sin(p/2 – b).
Тогда hB = PB + PK,
hC = hC – T; T = B0C/cosG; PB = PB0/cosG.
Для положения I, эти величины определяются аналогично.
b = p/2 – j + Q – G;
hB = PB – PK; hC = hB + T.
2. Для вогнутого контура, I положение. Расчетная схема аналогична, по этому γВ и RA тоже (рис. 3.26).
Определяем hB, hC, β.
Из DАОР найдем угол ОРА
Q = OPA = arcsin(AO/r).
Из DОВ0В; PB0 = PO + OB0; PO = PA∙cosQ = rcosQ;
B0PB = arctgB0B/PB0 = arctg3/2PB0.
b определением DАКР:
p/2 + b – КРА + j – КРА,
где КРА = Q – G; из DКАР найдем РК;
РК = rsin(j)/sin(p/2 – b).
Тогда hB = РВ – РК = РВ0/cosG – PK,
hC = hB + T; T = B0C/cosG.
3. Для положения II.
b = p/2 – j – Q – G; hB = PB – PK; hC = hB + T.
В результате всех этих расчетов были составлены программы для вогнутого и выпуклого контура, причём для двух положений механизма.
4. Определим область изменения φ в рис. 3.25
γВ = j – В0РВ = j – G;
B0PB = G = arctg(S/РВо) = 0,19 рад;
γВ = – 0,19 – + 2,95 рад.
В результате анализа получены следующие результаты:
Выпуклый контур. На рис. 3.27 построен график зависимости
RA(RC/RB). По сравнению с механизмом типа «тормозок – рейка» здесь RА меняется в значительно меньшем диапазоне от 0 до 2 H, а также разница RА между I и II положением меньше. В зависимости от радиуса кривизны r графика (рис. 3.28) реакция RА практически постоянна и изменяется в диапазоне 0,02 Н < RA < 0,37 H.
Характер кривых графика (рис. 3.29) показывает, что с увеличением отношения Rc/RB угол gВ уменьшается в меньшем диапазоне, чем в механизме типа «тормозок – рейка».
Вогнутый контур. Анализ результатов дает примерно то же, что для выпуклого контура, только характеристики его работы несколько хуже.
Из анализа следует:
– механизм типа «рейка – рейка» дает более устойчивые результаты при обработке выпуклого контура, чем механизм типа «тормозок – рейка»;
– этот механизм также позволяет обрабатывать вогнутый контур, что не может делать механизм типа «тормозок – рейка»;
– изменения RC и RA происходят в меньшем диапазоне;
– все это говорит о преимуществе механизмов типа «рейка – рейка» при обработке деталей различной конфигурации.
В. Разработка схемы и синтез двухреечного механизма ФТОУ-2
Процесс работы механизма
Любой контур можно представить как комбинацию дуг окружностей и прямых линий. Рассмотрим работу двухреечного механизма с различным перемещением и расположением направляющего упора при обработке деталей по краю трех возможных конфигураций.
1. Выпуклый контур (рис. 40)
Пусть в начале работы край детали не соприкасается с упором. За счет разницы перемещения I и II рейки деталь поворачивается вокруг МЦВ(Р) на угол a и ее край перемещается из положения (1-1) в (2-2). Здесь υС, υВ соответственно перемещения основной (1) и дополнительной (II) рейки, перемещение (υВ) дифференцировано и зависит от пружины. На длину стежка влияет перемещение рейки (1), т.к. игла расположена в прорезе основной (1) рейки. Деталь поворачивается до соприкосновения с упором.
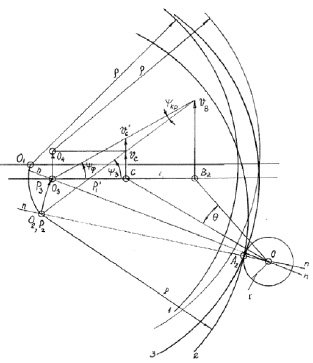
Рис. 3.31. Кинематический анализ ФТОУ-2
Рассмотрим процесс обработки детали, состоящей из двух сопряженных дуг радиусами ρ и r. Чтобы обеспечить Dmin и наименьшую ошибку эквидистантности строчки, МЦВ должен совпадать с центром дуги, которая в данный момент обрабатывается. Это достигается за счет уменьшения перемещения II рейки, которое становится υВ, перемещение I рейки остается тем же т.е. υC. Уменьшение перемещение достигается за счет того, что сила действия пружины, которая транспортирует эту рейку, уравновешивается силой давления детали на упор.
При обработке сопряженных контуров происходит перенос МЦВ (Р) из точки 01 в точку 02. За один поворот главного вала деталь поворачивается на угол a* < a и край детали из положения 1-1 сместится в положение 2-2.
2. Вогнутый контур (рисунок не приведен). Процесс аналогичен, только здесь υC > υВ, a* < a чем при вогнутом, здесь деталь как бы обрабатывается по упору.
3. Прямой контур (рисунок не приведен). Процесс аналогичен, но здесь перемещения основной и дополнительной рейки должны быть одинаковы, υC = υВ, следовательно, МЦВ находится в бесконечности и деталь перемещается без поворота. Контур (1-1) совпадает с (2-2).
На примере трех рассмотренных конфигураций можно рассмотреть все многообразия сложных контуров деталей. Таким образом, с помощью разрабатываемого механизма возможно, обрабатывать все виды кривизны.
Для разработки ФТОУ-2 выберем базовую машину 1022 М кл. В машине цепь вертикального перемещения не перетерпела никаких изменений. В цепи горизонтального перемещения вмонтирована дополнительная рейка, которая за счет большей длины шатуна, чем у основной, совершает большее перемещение. Это перемещение обеспечивается предварительной затяжкой пружины, которая закреплена на валу между основной и дополнительной рейкой. Вертикальное движение, получает за счет ползуна, который перемещается в направляющей. Направляющая, в свою очередь, связана с основной рейкой, которая связана с цепью вертикального перемещения.
4. Определение длины шатунов основной и дополнительной рейки.
Для обеспечения работоспособности применяется V1/V2 = 2–6;
V1 – скорость дополнительной рейки;
V2 – основной рейки.
При одинаковом t P:
S1/S2 = 2–6.
Пусть S1/S2 = 2; тогда считая S1 = (I1I2) и S2 = (L1 L2) получим I1I2/L1 L2 = 1/2, (рис. 3.32)
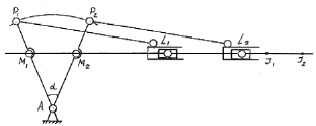
Рис. 3.32. К синтезу ФТОУ-2
В.1. Разработка кинематической схемы ФТОУ-2
M1M2/P1P2 = 1/2, примем Р1А1 = 24 мм, из подобия DАР1Р2 ~ DАМ1М2 находим:
АМ1 = АР1/2 = 12 мм,
где АМ1 – длина шатуна основной рейки; АР1 – II дополнительной рейки.
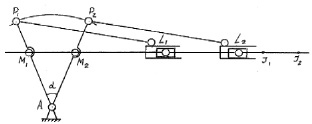
Рис. 3.33. К синтезу ФТОУ-2
Т.к. S определяется перемещением основной рейки М1М2 = 5 мм – (это максимальная длина стежка, обеспечиваюшая машиной 1022 М). Найдем угол качения шатунов, из DАМ1М2:
amax = 2arcsin∙M1M2/2AM1 = 2arcsin∙5/24 = 24°.
В.2. Синтез цепи горизонтального перемещения реек
Вследствие того, что радиус качения основной рейки уменьшен в два раза, то для выполнения технических условий заложенных в машине 1022 М кл. (т.е. Smax = 5 мм), угол качения шатуна увеличится до amax. По
технологии, длина стежка должна быть S = 2 мм, т.е. механизм вполне отвечает требованию технологии. Для использования на других операциях (Smax > 2 мм), рассмотрим пути увеличения (Smax).
Рассмотрим цепь АВСDKFO (рис. 3.34). Угол качения звена АВ составляет 12°, и достигается за счет эксцентрика OF эксцентриситетом:
e = FIFII/2 = 10/2 = 5 мм.
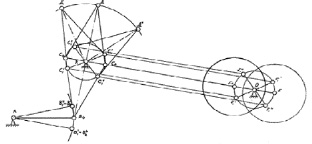
Рис. 3.34. К синтезу цепи горизонтального перемещения рейки
Рассмотрены три положения механизма: при прямом ходе, при обратном и когда перемещение равно нулю. Угол качения звена КД составляет 88° и он обеспечивает регулировку длины стежка. Увеличение угла качения звена АВ с 12 до 24° можно достичь различными способами:
а) уменьшением длины звена АВ. Этот способ не приемлем, т.к. он связан с переделкой всей цепи горизонтального перемещения реек.
б) путем изменения координат точки Д. Это изменение привело бы к изменению звеньев регулировки длины стежка, а также к увеличению угла качения звена КД, что не позволяет конструкция.
в) увеличением эксцентриситета (е). Это увеличение отразится также на увеличения угла качения звена КД, но не существенно.
Для определения увеличения эксцентриситета (е) проведем графический синтез шестизвенника цепи горизонтального перемещения реек
по двум положениям звена АВ. Длины звеньев АВ, СВ, КД, CF известны, положение точек К и О относительно А известно.
В результате графического синтеза получаем следующее: е = 7 мм, тогда увеличивается ∠ Д1КД11 = 98° (у базовой машины этот угол равен 88°); Увеличение угла Д1КД11скажется на изменении длины стежка. Из рис. 43 видно, что регулировка длины стежка представляет собой четырехзвенный механизм КТREH, причем КТ жестко связана с звеном КД. Увеличение угла Д1КД11 и, следовательно, угла Т1КТ11 может быть достигнуто за счет изменения угла q у базовой машины (∠q = 44, угол Д1КД11 = 88°). Следовательно, можно предположить, что увеличение угла Д1КД11 на 10° можно достичь за счет увеличения угла q на 5°, или от среднего положения точки Н на линии Н1Н11 по сравнению с базовым изменяется на 2,5°, что конструкция машины вполне позволяет без ее переделки.
В результате получены все размеры звеньев в цепи горизонтального перемещения реек. Далее определены параметры пружин ФТОУ-2, так как в конструкции сделаны изменения, т.е. в механизм транспортирующих реек введена дополнительная рейка, работа которой зависит от гибкой системы. Необходимо определить параметры пружины гибкой системы.
Таким образом:
– разработанный способ и устройство позволяют выполнять контурные строчки, не применяя программоносителей и специальных следящих систем. Ориентация деталей относительно иглы осуществляется с помощью механизма основной рейки и дополнительной рейки, снабженных гибкой системой;
– исследование и синтез механизма позволили выбрать параметры нового механизма, которые использованы при разработке ФТОУ-2 на базе машин 597, 22, 1022, 224 кл.