Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Баубеков С. Д., Таукебаева К. С.,
3.10.1. Сущность автоколебания детали в процессе ориентации
В процессе автоматической ориентации с применением ФТОУ возникают колебательные движения ориентируемой детали, сущность которого применительно для автоматизаций процесса ориентирования с использованием ФТОУ не изучена в известной литературе. Ниже приводим некоторые предположения о причинах возникновения автоколебаний, а также установим аналитическую взаимосвязь этого эффекта с выполняемой технологической операцией с применением ФТОУ.
Известно из [20], что после соприкосновений края детали с направляющим упором в процессе ориентирования ее, кромка детали деформируется на определенную величину и когда игла выходит из материала, то кромка детали резко выпрямляется в обратном направлении, поворачивая деталь назад, а в это время деталь еще перемещается роликами в направлении выполнения стежка (т.к. у машины 330-8 кл., ролики совершают непрерывное перемещение). Значит, край детали отходит от упора на величину деформации ∆, (см. рис. 3.20, раздел 3.6.3) подготавливая край детали к новому циклу-проколу иглой материала для образования стежка без деформированной кромки. Это обеспечивает выполнение контурной строчки эквидистантно краю детали. Этот эффект (в приведенной работе [84], эта проблема не рассмотрена) в процессе автоматического ориентирования деталей при выполнении контурной обработки назовем «автоколебанием» детали. В нашем случае, эффект автоколебания можно представить в виде релаксационного колебания [54], то есть накопление деформации, затем резкое изменение состояния и деталь возвращается в исходное первоначальное состояние; а в следующем цикле ориентации снова накапливается медленное изменение состояния и т.д.
Кулоново демпфирование в процессе ориентирования [54]. Кулонова сила трения не зависит от перемещения и его производных и для заданного скользящего тела есть величина постоянная. Следует помнить, что сила, требуемая для начала движения, обычно больше силы, необходимой для поддержания движения. Коэффициент трения не обязательно постоянен и зависит от чистоты поверхностей скользящих тел.
Свободные колебания системы с кулоновым трением показаны на рис. 3.20. Примем, что при x = 0, пружина находится в свободном состоянии (т.е. не прижата), это соответствует положению начала ориентации, когда кромка края детали не деформирована в момент контакта ее с упором (см. рис. 3.20, б), т.е. когда деталь поворачивается против часовой стрелки со скоростью (ω) с помощью ФТОУ. Уравнение движение массы (см. рис. 3.20) можно записать как [54]
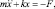при x > 0; (3.84)
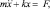при x < 0, (3.85)
где сила трения F определяется по формуле (3.64). Решение уравнений (3.84) и (3.85) имеет вид:
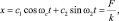(3.86)
где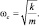 
Получено гармоническое колебательное движение, описываемое тригонометрической функцией в уравнении (3.86). Значения с1, с2 определяются начальными условиями, соответствующими некоторому моменту рассматриваемого движения.
Рассмотрим другой случай. Примем, что при t = 0, масса смещена из положения равновесия на величину Х0 и отпущена с нулевой начальной скоростью. При этом, движение слева направо можно выразить соотношением вида:
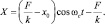(3.87)
Это уравнение справедливо при 
, что соответствует 0 ≤ ωct ≤ π.
За половину цикла ωct = π перемещение
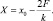(3.88)
А скорость 
. Следовательно, за половину цикла амплитуда уменьшается на величину 2F/k.
Таким образом, в случае свободных колебаний, полное уменьшение амплитуды за цикл равно 4F/k, так как показано на рис. 3.20, в (раздел 3.6.3). Если к массе приложена гармоническая сила, (в нашем случае см. формулу (3.65), определим Rop), то из уравнения [54]:
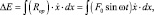(3.89)
можно определить рассеяние энергии за цикл при установившемся режиме. С другой стороны, если сила демпфирования имеет постоянную величину F(Rop), а полное перемещение за цикл равно 4х, то
∆E = 4FX. (3.90)
Эквивалентный коэффициент вязкого демпфирования получим, приравнивая ∆E в уравнениях (3.89), (3.90) [54]
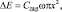(3.91)
т.е.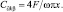 
(3.92)
Следует заметить, что С∂kβ не постоянная величина, как это обычно предполагается при вязком демпфировании, а зависит от частоты возмущения ω, от амплитуды колебания Хч, от величины F(Rop).
Амплитуду установившейся реакции можно получить из решения уравнения:
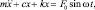(3.93)
подставляя С∂kβ из уравнения (3.92) вместо (С). Согласно уравнению [54]:
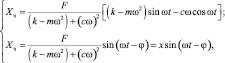(3.94)
где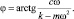 
Этo и есть амплитуда колебания детали при ориентации [116]
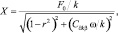(3.95)
где r = ω/ω0. Подставим (3.94) в (3.95) получим [54]
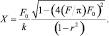(3.96)
Это уравнение дает действительное значение Х только когда 4F/πF0 < 0. Из (3.96) следует, что теоретически резонансная амплитуда всегда бесконечно велика. Резонансную амплитуду можно также вывести из энергетических соотношений согласно уравнению [20]
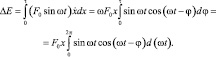(3.97)
Фазовый угол φ при резонансе равен 90°, а подводимая энергия составляет величину F0xπ. Рассеяние энергии (3.97) за цикл равно 4Fx отсюда, если 4F/πF0 < 1,0, то подвод энергии превышает рассеяние, причем излишек энергии идет на увеличение амплитуды колебания. Если система обладает сильным демпфированием, то движение нельзя полагать гармоническим и нужно произвести более точный анализ.
Таким образом, исследование позволяет сделать выводы, что при автоматизации контурной обработки швейных деталей с применением ФТОУ, имеет место автоколебание ориентируемой детали.
Автоколебание во многом зависит от кулоновой силы демпфирования, то есть силы сухого трения, возникающей между деталью и поверхностью игольной пластины, во время ориентированного перемещения детали. Используя известные методы оптимизации, получаем из формул (3.53) и (3.57) оптимальные величины h1, h2 и определяем реакции возникающих при автоматизированной ориентации детали с применением ФТОУ. Затем, из формул (3.91), (3.93), (3.94), (3.96), (3.97) с учетом сухого трения (кулоновой силы демпфирования) решаем задачу обеспечения наилучшего условия работы ФТОУ и соответственно принимаем необходимые решения для оптимизации параметров ФТОУ.