Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Баубеков С. Д., Таукебаева К. С.,
3.10.2. Автоколебания детали при упрощенной характеристике трения
В работе [20, 29, 54] рассмотрены способы решения задач об автоколебаниях, где использованы два упрощения:
1) о синусоидальном законе движения (для слабо нелинейных систем);
2) о безынерционности системы.
Однако, во многих случаях эти упрощения неприемлемы, так как закон автоколебаний в действительности существенно отличается от синусоидального, а движущиеся тела обладают значительной массой.
В нашем случае, в процессе ориентирования детали участвуют два инструмента и ограничительный (направляющий) упор [52]. На рис. 3.42, представлена схема автоматической ориентации детали с применением ФТОУ.
В процессе ориентации возможны следующие случаи:
а) если деталь имеет кривизну края (рис. 3.41, а, (+ρ), то за первую половину периода перемещения без иглы, край детали отходит от упора (то есть отрывается) на некоторую величину (∆). А (∆) зависит от величины деформации края детали упором и величины ρ(Vc < VB);
б) если край детали имеет кривизну (–ρ) (рис. 3.41, б), то край отходит от упора на величину (∆1), то есть на величину упругой деформации края детали об упор, но ∆1 < ∆упр, т.к. край детали не успевает полностью выпрямится, (Vc < VB); Здесь, после выхода иглы из материала, край натыкается на упор;
в) когда край детали прямая ρ = ∞, (рис. 3.41, в), здесь, после соприкосновения края детали с упором Vc = VB, деформация края детали упором ∆11 – min. Здесь после выхода иглы из материала, край не отходит от упора, т.к. деталь перемещается роликами прямолинейно.
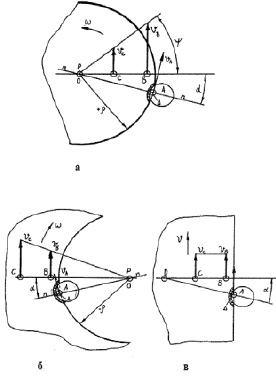
Рис. 3.41. Схема процесса ориентации деталей с различной кривизной:
где VB/VC > 3; α – угол расположения ограничительного упора; VB – скорость перемещения детали иглой; VC – скорость перемещения детали роликами;
ρ – кривизна края детали; VА – скорость детали в точке контакта края с упором; Р – мгновенный центр вращения детали; ω – угловая скорость вращения;
Ψ – необходимый угол поворота детали в процессе ориентации; n-n – нормаль, проведенная от центра кривизны (0) до точки контакта края с упором (точка А)
Рассмотрим случай (а), в момент ориентации детали с помощью ФТОУ, то есть при ориентации детали относительно направляющего упора инструментами В и С, причем отношения линейных скоростей заданы заранее Vc/VB ≥ 3 [84]. При ориентации деталь, имеющая определенную массу, поворачиваясь со скоростью (ω), ударяется об упор в точке А, в результате чего ее край деформируется на величину (∆). Здесь ФТОУ должно обеспечивать условия эквидистантности выполнения строчки по контуру детали
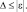
В работах [20, 29, 30] определены Rор – ориентирующая реакция с учетом сухого трения детали и игольной пластины (платформы) машины (рис. 3.42, а). Представим деталь (кожа опойка) упруго – эластичным материалом [20, 29]. Тогда расчетную схему (см. рис. 3.42, а) приводим к виду (рис. 3.42, б), где m – масса детали; Rор – ориентирующая реакция; g – ускорение свободного падения; Fk – сила сухого трения между деталью и пластиной; Na – нормальное давление детали на упор в точке А.
В процессе ориентации детали возникают Rор, Fk и Na (см. рис. 3.42, б), силы (реакции), необходимые для обеспечения постоянного контакта края детали с упором в точка А, то есть эти силы должны обеспечить условие неразрывности контакта края детали с упором в точке А
Rop ≥ Fk + Na. (3.98)
От воздействия ориентирующей реакции Rор (Rор > 0) в момент контакта с упором, край детали деформируется на величину (∆), т.е. пружина (см. рис. 3.42, б) деформируется на величину Х. Обозначим жесткость кожи опойки [20, 29] через (с).
Рассмотрим движение детали 3, связанной с пружиной 4 (это и есть деформированная часть края детали) (см. рис. 3.42).
Скорость детали будем считать в рассматриваемом случае постоянной и равной υ0 = ωρ. В нормальном режиме движение детали обладает общей скоростью υ0, причем сила упругости пружины Pп равна силе трения Fk. Если скорость υ0 мала, то малое случайное препятствие может оказаться достаточным для остановки детали. Рассмотрим, что происходит после этого.
ФТОУ заставляет поворачиваться деталь 3 со скоростью ω (см. рис. 3.42), продолжая движение вправо, прижимает пружину 4 до тех пор, пока сила сжатия пружины P не станет равной силе Rор и когда игла в точке (В2) выходит из детали, накопленная сила прижатия пружины Р «срывает» деталь, поворачивая ее в обратную сторону (–ω) (рис. 3.43, а) относительно точки (линии) прижатия детали роликами (С) на величину прижатия – деформации (∆1).
Здесь отход края детали от точки А происходит на величину деформации смятия края детали упором, а также на величину прогиба края (y1) (см. рис. 3.42, а). Последнее зависит от конструкции лапки – упора (см. гл. 3.6.3). Имея направляющие планки в конструкции лапки, осевой прогиб (y1)можно уменьшить. Так как ролики непрерывно (330-8кл) перемещают деталь (рис. 3.42, б), край детали отходит дополнительно на некоторую величину, которая зависит от ρ и s/2-шага стежка, в данном случае Sp = s/2, т.е. половина цикла перемещения осуществляется без участия иглы.
Рис. 3.42. а – схема к определению смятия края детали;
б – схема к определению упругой деформации края детали
На следующем этапе ориентированного транспортирования детали инструментами (С и В) деталь заново поворачивается против часовой стрелки (+ω) чем, обеспечивается контакт края детали с упором – направляющим в точке А на каждом этапе образования стежка и ориентирование детали с учетом «отскока» ее от упора в точке А, деталь восстанавливается и этот эффект называется релаксационным автоколебанием [54].
Итак, момент «срыва» примем за начало отсчета времени (t = 0). При этом равны нулю, как смещение Х, так и скорость детали 
, т.е. Х = 0;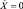 
.
При «срыве» нельзя предполагать мгновенного скачка скорости. Такому скачку соответствовали бы бесконечно большое ускорение, а следовательно, и бесконечно большие силы, так здесь, как в [54] на деталь в первый момент движения действует конечная сила R4–R2
(см. рис. 3.44, a); R1 – сила трения покоя (рис. 3.44, б); R2–R3, R4–R5 – силы, соответствующие точкам 2, 3, 4, 5.
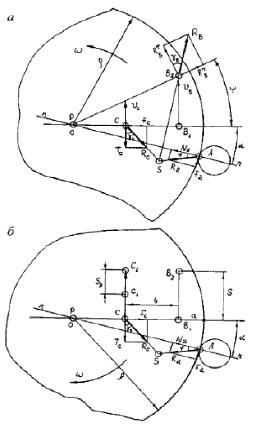
Рис. 3.43. Ориентирование детали:
а – инструментами В и С; б – инструментом С
а б
в г
д е
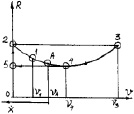
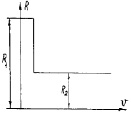
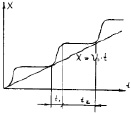
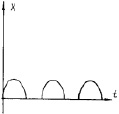
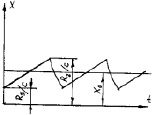
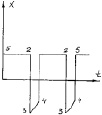
Рис. 3.44. Графики характера автоколебания:
а – график зависимости R(V) при автоколебании детали;
б – график зависимости R(V) во время «срыва» детали от игольной пластины; в – график характера движения детали; г – график характера скорости детали; д – характер автоколебания детали;
е – график изменения скорости детали при ее автоколебании
Тогда дифференциальное уравнение движения детали запишем в виде
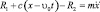(3.99)
или
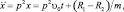
где р – частота свободных колебаний детали.
Решение этого уравнения, отвечающее нулевым начальным условиям, имеет вид [54]
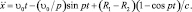(3.100)
Первое слагаемое правой части описывает основное движение со скоростью ведущего звена, а остальные слагаемые – дополнительные колебания детали. Скорость движения детали меняется по закону [54]
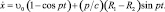(3.101)
Следующая остановка детали произойдет в момент, когда Х вновь обратится в ноль. Условие остановки 
приводит, согласно соотношению (3.101) к уравнению
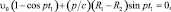
где t1 – время от момента срыва до новой остановки. Введем безразмерный параметр
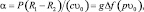(3.102)
где Δf – разность коэффициентов трения покоя и движения.
Условие остановки принимает вид
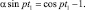
Решая это трансцендентное уравнение, находим:
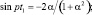
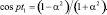(3.103)
Получив отсюда значение t1, можно по формуле (3.100) определить Х1, детали в момент новой остановки, т.е. путь, пройденный деталью за время t1
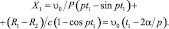
С учетом (3.100) найдем по формуле (3.99) силу сжатия пружины в момент остановки детали
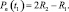
Так как R2 < R1, то Pп(t1) < R1. Следовательно, после остановки деталь будет оставаться на месте до тех пор, пока сила упругости пружины вновь не достигнет значения предельной силы трения покоя R1. Это совпадает со временем момента выхода иглы из материала детали в точке В2.
За время, в течение которого деталь покоится, сила сжатия пружины постепенно возрастает на величину (рис. 3.44, б),
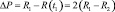
и соответствующее укорочение пружины составляет
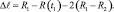
Такой же путь проходят инструменты (В и С) ФТОУ за время, пока деталь стоит на месте. Следовательно, длительность состояния покоя детали определяется как
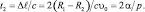(3.104)
Тот же результат можно найти из условия (рис. 3.53, в, г)
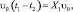
выражающего равенство перемещений детали и инструментов (В и С) ФТОУ за период ориентации.
Таким образом, период автоколебаний детали определяется формулой T = t1 – t2, для использования которой нужно сначала найти t1 из выражения (3.103), а затем t2 по формуле (3.104). В момент T = t происходит следующий срыв детали и начинается новый цикл автоколебаний. Характер движения показан на рис. 3.44, в, г.
Чем меньше скорость ведущего звена ФТОУ, тем более резко выражен процесс автоколебаний детали. Действительно, при малых значениях υ0 безразмерный параметр α становится весьма большим и из выражения (3.102) в этом случае следует [115]
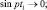
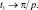
При учете выражения (3.104) период автоколебаний равен T ≈ (π + 2α)/р. Значения второго слагаемого в числителе увеличивается с уменьшением скорости υ0.
В совокупности, представленное исследование точнее объясняет причину явления процесса автоколебания детали при автоматизированном ориентировании ее с применением ФТОУ. Используя полученные результаты, процесс автоколебании детали можно представить в виде математической модели. Используя известные методы оптимизации, можно добиться получения требуемых величин параметров ФТОУ, обеспечивающих безотказную работу СМК.