Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
Баубеков С. Д., Таукебаева К. С.,
3.12.1. Определение деформации края детали
В работе [16] отмечено, что край детали подвергается пластической деформации. Однако пластическая деформации в данном случае будет незначительной, по сравнению с упругой, так что ее влиянием можно пренебречь. Предположим, что в процессе имеет место только упругая деформация кожи. Здесь торцевая деформация зависит от силы прижатия детали к упору, величины зоны контакта упруго – пластической деформаций края детали. Это явление носит случайный характер, т.к. сила прижатия к упору является переменной как по величине, так и по месту расположения. Физико-механические характеристики кожи различны. Поэтому установление точной зависимости между этими величинами не представляется возможным. Для выяснения ситуации используем методику приведенную в работе [16]. Но в эту методику введем условия работы ФТОУ, то есть рассматриваем автоматизированное ориентирование детали [35, 39, 40, 47].
Пусть упор задан в виде сектора с радиусом – ry (рис. 3.47).
Деталь прижимается к упору ориентирующей силой; ε0 = ε1 – ε2 – величина припуска. Итак, за начало координат принимаем точку 0 на дуге 0А и выделим элемент деформации df с координатой х, у. df деформируется под действием dNA. Элементарная величина смятия в направлении осей x и y может быть выражена через напряжение смятия и элементарные силы реакции, разложенные по оси x, y:
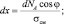
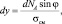(3.116)
где sсм – напряжения смятия на единице поверхности края детали.
Допустим, что существует закон пропорциональности между деформацией и приложенной силой
sсм = e∙Е;
e = (ε1 – eх)/e1; eх = e2 + х, (3.117)
где e – относительная деформация; Е – условный модуль упругости участка; ε1 – величина припуска до выполнения краевой строчки; ε2 – величина припуска в точке 0; eх – величина припуска во время строчки.
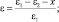
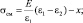
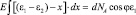
при x1 = 0, x2 = ε1 – ε2
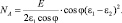(3.118)
С учетом (3.116)
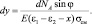
Тогда
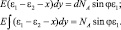(3.119)
Предел интеграла х = 0 и х = ОА = АВ = rysinα0.
Как дуга окружности, где α0 – угол обхвата боковой поверхности упора, а также угол, определяющий направления ориентирующей реакции ФТОУ.
Тогда
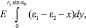
где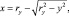 
заменяя в интеграле х, запишем
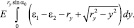(3.120)
Разность ε1 – ε2 = xmax, тогда
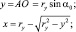
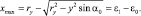
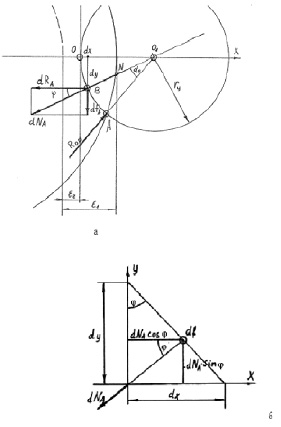
Рис. 3.47. К определению торцевой деформации детали:
а – расчетная схема; б – к определению dNA
Подставляя эти значения, в интеграл (3.120) и решив его, получим
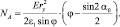(3.121)
В соответствии с рис. 3.47, а, без учета силы трения детали о стол
Rop = NAcosα0. (3.122)
Тогда из (3.121) запишем как
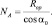(3.123)
Из равенства (3.121) и (3.122)
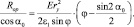
Откуда
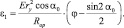(3.124)
Исследование (3.124) дает возможность получить рациональные параметры упора, с учетом сухого трения, так как здесь при определении ε1 учитываются наряду с другими факторами и Rop.
Из условия постоянства контакта края детали с упором, а также обеспечения минимальной деформации края детали упором (чего должно обеспечивать ФТОУ, см. условия (3.61). гл. 3.6.3), считаем постоянным NА и Е. Тогда выражение (3.124) имеет следующее решение
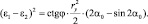(3.125)
Откуда деформация края
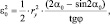(3.126)
если считать
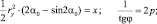
то
y2 = 2px. (3.127)
Таким образом, величина деформации края детали зависит от кривизны упора, угла обхвата и угла подачи материала по отношению к касательной к работе поверхности упора. Это представляет как парабола функцию (3.127).
Итак, в результате теоретического исследования установлено, что упоры надо располагать впереди с поворотом на угол a, который уравновешивает поворот детали, вызываемый парой сил при ориентировании с применением ФТОУ; выведена математическая зависимость деформации края детали от угла подачи материала, по отношению к касательной и рабочей поверхности упора, размеров сопрягаемых поверхностей края детали, рабочей поверхности приспособления при условии, что прижимная сила прижатия и транспортирования, также жесткость материала детали являются постоянными; получена математическая зависимость реакции упора на торец детали, обеспечивающая минимальную деформацию края детали; возможность деформации края детали увеличивается с увеличением угла х и величины линии контакта; увеличение ориентирующей силы Rop ведет к увеличению деформации края.
Для подтверждения правомочности приведенных теоретических предпосылок о технологических возможностей вновь разработанных СМК на базе различных ФТОУ, проводены экспериментальные исследования для изучения безотказности и качественного выполнения контурных операции с применением разработанных СМК [39, 40, 48].