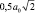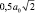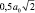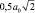Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

ОТ ЧЕТЫРЕХ К ОДНОМУ. СИЛЫ ВНУТРИАТОМНОГО ВЗАИМОДЕЙСТВИЯ И ПРОЧНОСТЬ МАТЕРИАЛОВ

Бадамшин И. Х.,

1.3. Предел упругости

Рассматривается теоретический метод расчета предела упругости бездефектных монокристаллов. Нитевидные кристаллы – «усы», входящие в состав эвтектических композитов в виде армирующей фазы, представляют собой пример практической реализации бездефектных монокристаллов.

Типичная экспериментальная зависимость изменения напряжения от деформации для нитевидных кристаллов – «усов» имеет следующий вид, в частности, для кристалла меди Cu, (рис. 1.27). Характер кривой является типичным для идеальной кристаллической решетки [20].

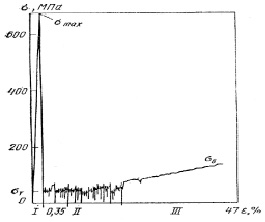
Рис. 1.27. Диаграмма растяжения нитевидного кристалла меди [21, 22]

«На диаграмме «напряжение – деформация» имеется ярко выраженный зуб текучести (стадия I). По достижению максимального напряжения sMАХ, соответствующего вершине зуба текучести, в кристалле начинается пластическая деформация: зарождаются и размножаются дислокации, образуются линии скольжения (Чернова–Людерса); увеличивается плотность дислокации, они выходят на поверхность и, как следствие всего этого, напряжение резко падает до значений sТ. На стадии II происходит движение дислокации (распространение линий скольжения) при постоянном напряжении. Пики напряжений свидетельствуют о зарождении новых линий скольжения, а минимумы – об их выходе на поверхность. С увеличением степени деформации наступает стадия деформационного упрочнения (III). Разрушение происходит при напряжении, которое по величине соответствует пределу прочности массивных монокристаллов.

Из приведенного анализа диаграммы растяжения следует, что прочность нитевидного кристалла характеризует верхний предел текучести sMАХ, а не предел прочности. Верхний предел текучести определяет максимальную прочность нитевидного бездислокационного кристалла, а образование в нем дислокации уменьшает его прочность до значений, характерных для обычных кристаллов. На основе полученных значений sMАХ и зная кристаллографическую ориентировку оси нитевидного кристалла
(направление роста), можно рассчитать напряжение сдвига tMАХ» [22]. В механике деформируемого твердого тела для обозначения sMАХ принят термин – предел упругости.

Однако существующие методы расчета определяют лишь порядок величины напряжения сдвига tMАХ. Например, модель Я.И. Френкеля, где напряжение сдвига t изменяется по закону [22]

t = sin (x /a0),

где а0 – период кристаллической решетки. А также модель Маккензи [23], по которой, в частности, для объемно-центрированной (ОЦК) и гранецентрированной (ГЦК) кубических решеток τmах определяется по формулам:

– для ОЦК решетки τmах = G/8 – G/10 = (0,125 – 0,100)G ≈ 0,110G;

– для ГЦК решетки τmах = G/22 – G/30 = (0,045 – 0,033) G ≈ 0,039G,

где G – модуль сдвига.

В работе решается задача определения предела упругости в следующей последовательности.

Допущения

Известно [24], что силы упругости в твердом теле обусловлены кулоновскими силами межатомного взаимодействия.

Формула расчета предела упругости выводится на основе моделей кристаллографии и закона Кулона. При этом в условиях равновесия сил притяжения и отталкивания в кристаллической решетке решается статическая задача.

1. Используется геометрическая часть модели Я.И. Френкеля [22]. В частности, на рис. 1.28 показан этап формирования дислокации и условие равновесия кулоновских сил притяжения и отталкивания, когда t = 0 при b/2.

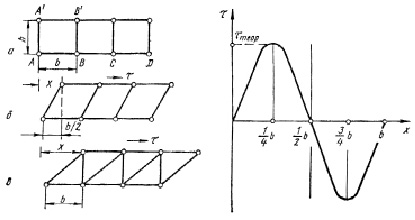
Рис. 1.28. Иллюстрация модели Я.И. Френкеля, причем b ≡ a0 [22]

2. Рассматривается элементарная атомная ячейка простой кубической, объемно-центрированной и гранецентрированной кристаллических решеток.

3. В условиях равновесия сил притяжения и отталкивания зарядов, а также отсутствия внешней силы в простой кубической решетке в кристаллографическом направлении [100] кулоновская сила F0 определяется по известной формуле

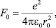
где r0, м – расстояние между зарядами при отсутствии внешней силы. В частности, для плоскости (100) простой кубической решетки r0 = a0.

Если прилагать внешнюю силу сдвига F в кристаллографическом направлении [100] в пределах от 0 до некоторой величины приращения DF, то расстояние между атомами будет увеличиваться до значений r = a0 + ∆r, где r, м – расстояние между взаимодействующими зарядами в кристаллографической плоскости (100). Атом переместится из положения 1 в положение 2 (рис. 1.29).

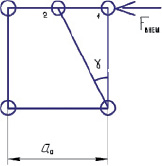
Рис. 1.29. Схема смещения атомов в простой кубической решетке

Тогда тангенциальное напряжение сдвига определяется как t = F/А, где А, м2 – площадь сдвига.

Связь между нормальной и тангенциальной проекциями напряжения сдвига бездефектного монокристалла определяется по формуле [25]

σmax = τmax /(cos α⋅cos b),

где α – угол между горизонтальной плоскостью и плоскостью сдвига; b – угол между плоскостью сдвига и направлением нормального напряжения.

В частности, для грани куба или плоскости (100) нормальная составляющая предела упругости равна тангенциальной sMAX = tMAX.

Разрыв межатомной связи при сдвиге произойдет при DFmax < F0, с соответствующими значениями межатомного расстояния ∆r = r – a0 и максимального угла сдвига γ/2 = γmax в соответствии с геометрической частью модели Я.И. Френкеля, тогда как разрыв межатомной связи при отрыве произойдет при DFmax = F0.

Угол γ соответствует положению атома b/2, а угол γmax соответствует положению атома b/4 (рис. 1.28).

В условиях сдвига происходит процесс, описанный в модели Френкеля, т.е. нарушение равновесия и передача связи другой паре атомов. При F < DFmax нарушается только равновесие атомов. Межатомная связь не разрывается.

Таким образом, для вывода из равновесия атомов при сдвиге необходимо некоторое приращение силы DF, отличное от нуля. При этом величина предела упругости, в частности, будет определяться значением угла γmax.

4. Для плотноупакованных кристаллографических плоскостей (100), (110) и (111) максимальный угол сдвига γmax различается (рис. 1.30).

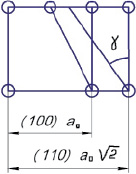
Рис. 1.30. Схема смещения атомов в простой кубической решетке в плоскостях
(100) и (110)

В частности, у простой кубической решетки для плоскости (100)

γmax = 0,5arctg(0,25) = 28°/2 = 14°,

а для плоскости (110)

γmax = 0,5arctg(0,25) = 38°/2 = 19°.

Результаты расчета геометрических параметров решетки при сдвиге приведены в табл. 1.14.

Таблица 1.14

5. Максимальная площадь сдвига не превышает 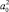, т.е.

.

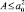В частности, для плоскости (110) площадь 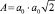, но принимается 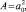т.к. в противном случае объем рассматриваемой элементарной ячейки составит

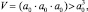
и нарушаются размер и периодичность бездефектного монокристалла.

Таким образом, после подстановки значения кулоновской силы в соотношение t = F/А при различных углах сдвига атома из положения 1 в положение 2 (рис. 1.29), в общем случае формула тангенциальной составляющей предела упругости имеет вид [26, 27]

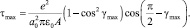(1.1)

Пример расчета предела упругости

Площадь сдвига S определяется для кристаллографических плоскостей (100), (110), (111) простой, гранецентрированной и объемно-центрированной кристаллических решеток из геометрических построений. В частности, для плоскости (100)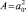

Максимальный угол сдвига определяется также из геометрических построений кристаллической решетки и составляет, в частности, для плоскости (100) гранецентрированной и объемно-центрированной кристаллических решеток γmax = 10° (табл. 1.14).

Результаты расчета тангенциальной составляющей предела упругости τmax по формуле (1.1) для монокристаллов некоторых металлов приведены в табл. 1.15. В частности, для железа Fe период кристаллической решетки a0 = 2,8665⋅10–10м, а γmax = 10°.

Таблица 1.15

Из табл. 1.15 видно, что результаты расчета дают удовлетворительную сходимость с результатами эксперимента. Так, расчетное значение тангенциальной составляющей предела упругости серебра Ag в плоскости (100) составляет 172 МПа, а экспериментальное – 160 МПа, расхождение расчета – 7,5 %.

Выводы

1. Выведена формула теоретического расчета тангенциальной составляющей предела упругости для монокристаллов. Получена удовлетворительная сходимость теоретических результатов расчета предела упругости с экспериментальными данными других авторов.

2. Выведенная теоретическая формула предела упругости позволяет получить исходные данные для оценки напряженно-деформированного состояния лопаток из эвтектических композитов (по одному из его компонентов), причем в условиях ограниченного объема экспериментальных данных.