
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.5. Предел текучести
В настоящее время предела текучести определяется, как правило, экспериментальными методами.
Экспериментальная зависимость изменения напряжения от деформации для нитевидных монокристаллов – «усов» – имеет вид (в частности, для монокристалла Cu), представленный на рис. 1.26.
В работе предлагается модель диаграммы «напряжение – деформация» нитевидных монокристаллов, основанная на электростатической природе упругости.
В основу расчета положены следующие допущения.
1. Рассматриваются бездефектные кристаллические решетки металлов, исследованные экспериментально в виде нитевидных кристаллов – «усов», которые деформируются пластически [20].
2. Используется геометрическая часть модели Френкеля [22].
3. Максимальное напряжение сдвига или предела упругости определяется по модели, приведенной в разделе 1.3.
4. Под пределом текучести понимается определение, общепринятое для металлов. Причем для нитевидных монокристаллов принимается среднее значение предела текучести по отклонениям на диаграмме «напряжение – деформация» (рис. 1.26).
5. Связь между нормальной и тангенциальной проекциями напряжения сдвига бездефектного монокристалла определяется по формуле [22]
sмах = tмах /(cos α⋅cos b), (1.2)
где a – угол между горизонтальной плоскостью и плоскостью сдвига; b – угол между плоскостью сдвига и направлением нормального напряжения.
6. Решается статическая задача на основе закона Кулона
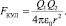
Теоретическая зависимость изменения напряжения от деформации для нитевидных кристаллов – «усов», предложенная автором, представлена на рис 1.33 и отличается от экспериментальной [21] участком 2–3.
В основе сил упругости лежат межатомные взаимодействия электростатической природы [24, 33]. Поэтому участок 2–3 на рис. 1.33 моделируется с помощью закона Кулона и определяется степенной функцией с целым отрицательным показателем вида y = c/x2, так как
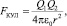
где FКУЛ – кулоновская сила взаимодействия между зарядами Q1 и Q2; r – расстояние между взаимодействующими зарядами. Но напряжение пропорционально силе, т.е. s (или t) ~ FКУЛ, следовательно, в окончательном виде [34, 35] участок 2–3 на рис. 1.33 определяется функцией
t = c/(x/a0)2, (1.3)
где a0 – период кристаллической решетки; x/a0 – угловая деформация при сдвиге простой кубической решетки.
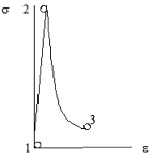
Рис. 1.33. Теоретическая модель диаграммы растяжения
нитевидного монокристалла
Из соотношения (1.2) определяется нормальная проекция напряжения сдвига – предела текучести.
В точке 2 напряжение s = sмах (соответственно тангенциальное напряжение t = tмах) – это так называемый «зуб текучести». В точке 3 напряжение равно пределу текучести s = sт (соответственно t = tтек), при котором монокристалл переходит в поликристалл за счет формирования дислокаций.
Таким образом, зная координаты точки 2 (значения tмах и x/a0 из раздела 1.3) и вид функции (1.3), вычисляется коэффициент с, а затем определяют координаты точки 3, т.е. значение tтек по величине деформации х = 0,5а0, определяемой по Френкелю. В соответствии с моделью Френкеля в точке с координатой х = 0,5а0 теоретическое значение напряжения сдвига равно нулю t = 0, т.е. атомы находятся в неравновесном состоянии, но на практике (рис. 1.26) [22] пластическое течение происходит при некотором постоянном значении напряжения sт (или tтек).
Таким образом, участок 2–3 имеет координаты [0,07а0; 0,5а0] по оси абсцисс.
Результаты расчета напряжения сдвига в точке 3, т.е. предела текучести tтек, приведены в табл. 1.17.
В соответствии с диаграммой «напряжение – деформация» (рис. 1.26), начиная с предела текучести, вследствие зарождения дислокаций монокристалл переходит в поликристалл, поэтому значения предела текучести монокристалла и поликристалла одинаковы. Это позволяет сравнивать результаты расчета для монокристаллов с экспериментальными значениями предела текучести поликристаллов. Данное сравнение допустимо, в частности, для недеформированных поликристаллов (технических и отожженных).
Как видно из табл. 1.17, результаты расчета удовлетворительно сходятся с результатами экспериментов.
Таблица 1.17
|
Наименование элемента, плоскость скольжения |
Величина tтек, МПа |
Погрешность, % |
Источник |
|
|
расчетная |
эксперимент. |
|||
|
Cu (ГЦК) (100) |
58,7 |
18*…60 |
– |
[20, 21] |
|
Ag (ГЦК) (100) |
36,0 |
40 (32,3 отожжен.) |
10 |
[20] [7] |
|
Cd (ГП) (0001) |
10 |
5* (9,81) |
– |
[20] [7] |
|
Fe (ОЦК) (100) |
148 |
(177 технич.) (123 отожжен.) |
– |
[7] |
Примечания: * – в экспериментальных данных не указана кристаллографическая плоскость скольжения, поэтому погрешность не рассчитывалась; в скобках указаны экспериментальные значения для недеформированных, с точки зрения технологии изготовления, поликристаллов (технических и отожженных).
Таким образом, зная значение максимального напряжения сдвига, можно рассчитать величину предела текучести для монокристаллов как металлов, так и неметаллов, например, карбидов и нитридов. Результаты работы можно использовать в практических расчетах на прочность бездефектных монокристаллов, в частности, для эвтектических композиционных материалов с нитевидными монокристаллами, используемых в рабочих лопатках газовых турбин, а также для недеформированных (с точки зрения технологии изготовления) поликристаллов.
