
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.6.3. Плотность кристаллических структур
В расчетах на прочность лопатки турбины необходимо знать плотность материала. В частности, ее величину для матрицы и армирующей фазы эвтектического композита лопатки, чтобы оценить величину объемных сил инерции при вращении рабочего колеса турбины. Решение данной задачи является одним из этапов обобщенной модели прочности лопатки [41] (рис. 1.39).
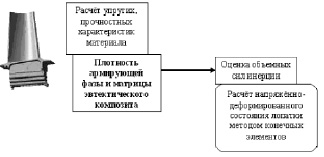
Рис. 1.39
В данном разделе обосновывается расчет плотности монокристаллов.
Плотность монокристаллов r определяется по известной формуле
r = m/V,
где m – масса; V – объем.
В рассматриваемом случае в качестве объема принимается объем элементарной атомной ячейки с периодом кристаллической решетки a0, равный
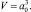
Масса элементарного объема определяется по следующей формуле:
m = mАMедkр,
где mА – атомная масса элемента; Mед = 1,66⋅10–27 кг – атомная единица массы; kр – коэффициент ретикулярной плотности для элементарной атомной ячейки (рис. 1.40).
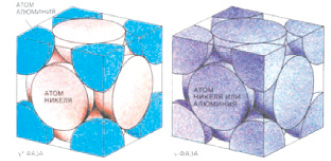
Рис. 1.40. Схема формирования ретикулярной плотности в ячейке [42]
Коэффициент ретикулярной плотности элементарной ячейки кристаллической структуры определяется в соответствии с правилами кристаллографии [43].
Тогда формула расчета плотности монокристалла, разработанная автором, примет следующий вид [44]
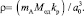
Плотность монокристалла простого вещества, состоящего из атомов одного химического элемента железа – Fe с объемно-центрированной кристаллической решеткой, определяется как
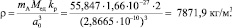
Плотность монокристалла простого вещества, состоящего из атомов одного химического элемента меди – Cu с гранецентрированной кристаллической решеткой, определяется как
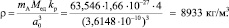
Плотность сложных веществ или соединений, состоящих их атомов разных химических элементов типа NaCl, определяется как сумма плотностей составляющих химических элементов, т.е.
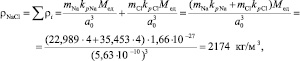
где kрNa, kрCl – коэффициент ретикулярной плотности соответственно для Na и Cl; mNa, mCl – атомная масса соответственно для Na и Cl; a0 – период кристаллической решетки NaCl (табл. 1.20).
Таблица 1.20
|
Символ элемента, |
Величина плотности r, кг/м3 |
Расхождение, % |
|
|
расчетная |
экспериментальная |
||
|
Fe |
7871,9 |
7872 |
0 |
|
Cu |
8933 |
8933 |
0 |
|
NaCl |
2174,5 |
2100 |
3,5 |
Из табл. 1.20 видно, что расчетная величина плотности для железа Fe составляет 7871,9 кг/м3, а экспериментальное значение – 7872 кг/м3 [7].
Результаты некоторых расчетов плотности приведены в табл. 1.21.
Таблица 1.21
|
Наименование |
Величина плотности, кг/м3 |
Погрешность, % |
Источник |
|
|
расчетная |
экспериментальная |
|||
|
Mo (ОЦК) |
10219,9 |
10218 (10200) |
0,02 |
[7] |
|
W (ОЦК) |
19248,5 |
19263 (19230) |
0,08 |
[7] |
|
Ta (ОЦК) |
16678,6 |
16623 (16600) |
3,3 |
[7] |
|
Nb (ОЦК) |
8581,5 |
8630 (8570) |
5,6 |
[7] |
|
TaС (кубич) |
14625,0 |
14500 |
8,6 |
[7] |
Примечание. Приведены рентгеновская и пикнометрическая (в скобках) экспериментальные значения плотности.
Как видно из табл. 1.20, 1.21, результаты расчетов удовлетворительно сходятся с результатами экспериментов.
Таким образом, результаты расчета применимы для оценки плотности моно- и поликристаллов, в том числе соединений, по которым редко или совсем не встречается справочная информация.
Результаты расчета плотности моно- и поликристаллов, из которых состоит матрица эвтектических композитов, являются исходными данными для моделирования прочности лопаток газовых турбин.
