Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.7.2. Обоснование расчетной модели коэффициента интенсивности напряжений
В отличие от моделей механики сплошной среды разработанная модель, учитывающая кулоновские силы межатомного взаимодействия в кристаллической решетке, позволяет оценить величину напряжений в вершине трещины.
Допущения
1. Физической основой расчетной модели являются электростатические силы притяжения и отталкивания между узлами кристаллической решетки, определяемые законом Кулона
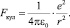
2. За расчетную формулу КИН принимается соотношение, основанное на концентрации напряжений [45]
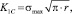
где σmax, r – максимальное напряжение и радиус скругления в вершине трещины (π⋅r – длина полуокружности в вершине трещины). Причем это не «приводит к бесконечным напряжениям и бесконечным градиентам напряжений в конце тонкого разреза», так как в основу расчета заложены конечные значения кулоновских сил в вершине трещины.
3. Используется известное положение о том, что КИН «не зависит от длины трещины, формы тела и схемы действующих нагрузок». Поэтому рассматривается модельная нанотрещина следующей геометрии (рис. 1.41, а). «В модели жестких сфер нерелаксированная идеальная граница совпадающих узлов не может соответствовать минимум энергии. Чтобы уменьшить сумму энергий соседних кристаллов необходимо сместить кристаллы один относительно другого. Хотя границы совпадающих узлов после указанного смещения зерен уже не существует, периодичность строения границ сохраняется и сохраняется сегмент повторяемости p (рис. 1.41, б), равный соответствующему сегменту идеальной границы совпадающих узлов (рис. 1.41, а)» [43].
Результаты расчета коэффициента интенсивности напряжения с учетом кристаллографического направления и поликристаллического состояния (равноосной структуры) для некоторых металлов приведены в табл. 1.22.
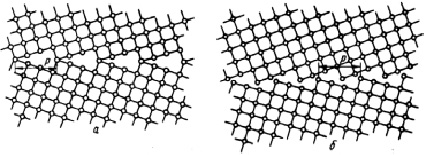
Рис. 1.41. Наклонная граница 37 <001> между зернами с кубической решеткой
в положении совпадения (а) и после жесткой релаксации (б)
Таблица 1.22
|
Наименование |
Величина коэффициента интенсивности |
Источник |
|
|
расчетная |
справочная |
||
|
Cu ⟨001⟩ Cu ⟨110⟩ Cu ⟨111⟩ Cu поликрист. Сплавы Cu |
42,7 64,2 75,5 60,8 – |
– – – – 50…110 |
– – – [49] |
|
Al ⟨001⟩ Al ⟨110⟩ Al ⟨111⟩ Al поликрист. Cплавы Al |
35,3 53,0 62,4 50,3 – |
– – – – 10…60 |
– – – – [49] |
|
Fe ⟨001⟩ Fe ⟨110⟩ Fe ⟨111⟩ Fe поликрист. Стали |
33,7 44,1 43,4 40,7 – |
– – – – 20…150 |
– – – – [49] |
|
Ni ⟨001⟩ Ni ⟨110⟩ Ni ⟨111⟩ Ni поликрист. Cплавы Ni |
59,7 89,6 105,5 84,9 – |
– – – – 60…110 |
– – – – [49] |
Поскольку экспериментальных значений КИН для монокристаллов металлов в справочниках не удалось найти, то результаты расчета сравниваются со значениями для сплавов на основе соответствующего металла. Из табл. 1.22 видно, что такая приближенная оценка укладывается в диапазон справочных данных.