
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.1.2. Модель нагружения вращающегося ротора
Для решения поставленной задачи разработана модель поступательного движения вращающегося тела.
Задача решается на примере совместного поступательного и вращательного движения тела – шара.
Допущения
1. Используется принцип суперпозиции.
2. Рассматривается равноускоренное движение центра масс тела по окружности в инерциальной системе координат XOY с центром в точке О (рис. 2.6): 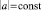 , изменяется только направление вектора ускорения.
, изменяется только направление вектора ускорения.
3. Решается первая задача механики: при заданной траектории движения определить действующие силы.
Соответствие положениям теоретической механики
Допустим, к телу приложены постоянные по величине внешняя сила F1 в центре масс точке С, направленная по касательной к окружности, и момент пары сил (F2,F2’) (рис. 2.6, а) В результате тело движется плоскопараллельно, а центр масс (точка С) – равномерно по окружности. Такое движение описывается системой дифференциальных уравнений [73]
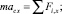 (2.1)
(2.1)
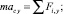 (2.2)
(2.2)
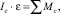 (2.3)
(2.3)
где m – масса тела; а = dV/dt – ускорение центра масс поступательного движения; Ic – момент инерции центра масс; Fi – внешние силы; e – угловое ускорение; Mc – момент сил относительно центра масс.
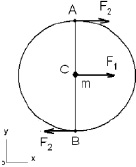
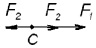
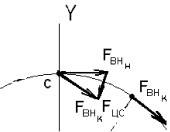
а б в
Рис. 2.6. Схема действующих сил
Рассмотрим движение центра масс – точки С по окружности (рис. 2.6, б, в). В соответствии с теоремой о движении центра масс момент от пары сил F2 равен нулю (рис. 2.6, б). В этом случае вращательная часть движения не рассматривается, а уравнение (2.3) не используется. Тогда сумма внешних сил, действующих на точку С, равна
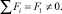
Схема сил на рис. 2.6, в получена путем параллельного переноса суммарного вектора внешних сил из конечного Fвнк в начальное положение Fвнн на бесконечно малой дуге перемещения. Откуда видно, что центростремительная сила является результирующей действия внешних сил, т.е. эквивалентна одной центральной силе Fц, вызывающей движение тела по окружности.
Для материальной точки С система (2.1)–(2.3) принимают следующий вид:
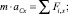 (2.4)
(2.4)
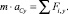 (2.5)
(2.5)
При переходе к одной центральной силе соотношения (2.4)–(2.5) можно записать в следующем виде:
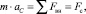 (2.6)
(2.6)
где ac = dVx / dt + dVy /dt. (2.7)
Таким образом, теорема о движении центра масс позволяет исключить из рассмотрения все наперед неизвестные внутренние силы [73] для упрощения решения задачи. Однако в решении данной задачи важно показать физическую сущность внешних и внутренних сил, определяющих движение тела по заданной траектории, что отражено в последующих пунктах допущений.
4. Движение точки С по дуге DE моделируется кусочно-линейной траекторией DKE, которая на бесконечно малом отрезке времени стягивается в дугу DE, определяя перемещение центра масс (рис. 2.7). Тогда
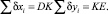
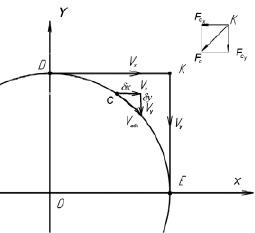
Рис. 2.7. Схема движения центра масс
То есть DK и KE – суммарные проекции на оси OX и OY элементарных линейных перемещений соответственно.
Так как проекции центральной силы Fcx и Fcy – переменные величины (рис. 2.7), то точка С перемещается по суммарным отрезкам DK и KE с переменным только по направлению и постоянным по модулю ускорением
ax = a⋅sinj; ay = a⋅cosj,
где j – угловое перемещение т. С.
5. Кусочно-линейная модель позволяет свести динамическую задачу, описываемую соотношениями (2.1)–(2.3), к задаче прямолинейного равноускоренного (меняется только направление) движения точки под действием проекций центральной силы. Тогда на отрезках DK и KE ускорение определяется по известной формуле
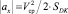
и
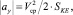
где SDK и SKE – длина отрезков DK и KE. Поскольку SDK = SKE и средние скорости также равны, то 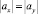 .
.
Такой же результат можно получить на основе закона сохранения энергии.
В соответствии с положениями механики [74], приращение кинетической энергии частицы dK на некотором перемещении равно алгебраической сумме работ всех сил dA, действующих на частицу на том же перемещении
dK = dA. (2.8)
Соотношение (2.8) справедливо в инерциальной и неинерциальной системах координат [74].
Под действием проекции силы Fcx центр масс перемещается с постоянным отрицательным ускорением по отрезку DK, а под действием проекции силы Fcy центр масс т. С изменяет направление и перемещается по отрезку KE с постоянным положительным ускорением.
На отрезке ДК под действием проекции внутренней силы Fcx внешняя сила F1 уменьшается и в точке К проекция скорости Vx = 0, кинетическая энергия также равна нулю. При этом совершаемая работа и, как результат, потенциальная энергия в точке К равна
Пx = Ax = F1⋅SDK .
В соответствии с моделью в точке К центр масс тела изменяет направление и движется по отрезку KE с постоянным положительным ускорением, равным ay. Причем в этой точке тело обладает потенциальной энергией Пx = Пy, т.е. можно записать, что по модулю
F1⋅SDK = Fcy⋅SKE
или
max⋅SDK = may⋅SKE.
Но из геометрических построений расстояния S = OD = DK = KE одинаковые и масса также одинаковая. Следовательно,
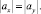
Причем
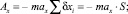
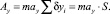
Тогда для прямолинейного равноускоренного перемещения материальной точки С по суммарным отрезкам DK и KE (рис. 2.7) можно записать соотношения
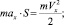
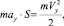 (2.9)
(2.9)
где Vx, Vy – средние значения проекций скорости. При этом результирующие значения работы и энергии на дуге DE равны нулю, что не противоречит исходным данным.
Поскольку 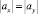 или
или 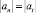 , то базовая формула расчета центростремительного ускорения центра масс (т. С), которое определяет движение тела по траектории DKE, имеет вид
, то базовая формула расчета центростремительного ускорения центра масс (т. С), которое определяет движение тела по траектории DKE, имеет вид
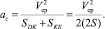 (2.10)
(2.10)
6. При моделировании движения центра масс тела – точки С – по окружности (в частности, по дуге DE) кусочно-линейной суммарной траекторией DKE, которая в пределе стягивается в дугу DE, ускорение определяется по соотношению (2.10). Проекции скоростей на оси координат изменяются следующим образом (рис. 2.7):
1) при перемещении из точки D в точку K под действием силы Fc,x проекция Vx изменяется от Vmax до 0, а проекция Vy = 0;
2) в точке K скорость равна нулю: Vx = 0; Vy = 0, изменяется направление движения за счет вращения тела Vmin = 0;
3) при перемещении из точки K в точку E под действием силы Fcy проекция Vx = 0, а проекция Vy изменяется от 0 до Vmax.
Так, на суммарном отрезке DK абсолютная скорость Vабс = Vx и изменяется от Vmax до 0, а на суммарном отрезке KE абсолютная скорость Vабс = Vy и изменяется от 0 до Vmax.
Таким образом, определена динамика движения по окружности точки С, которая определяет движение всего тела (шара), но не учитывает его вращение.
Кроме того, определены экстремальные значения скорости Vmax и Vmin.
7. При переходе от движения точки С к движению шара в целом, эпюры скоростей показаны на рис. 2.8, а–в.
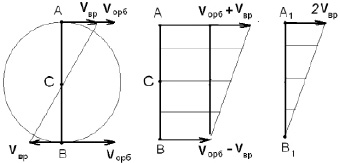
а б в
Рис. 2.8. Эпюры скоростей
В частности, для вращательной части движения шара эпюра скоростей представлена рис. 2.8, в.
Для кинематического анализа сложного движения шара и определения среднего значения ускорения (а следовательно, и скорости) используется теорема Шаля: всякое перемещение свободного твердого тела из одного положения в другое за время ∆t может быть осуществлено посредством поступательного его перемещения, равного перемещению некоторой точки тела и повороту около этой точки (рис. 2.9) [75]. Причем вращение тела вокруг неподвижной точки можно свести к рассмотрению движения двух точек [75], например, точек А и В.
В качестве «некоторой точки», т.е. полюса, принимается точка В. Если рассматривать движении тела по составляющим на некотором малом участке В1В2 (рис. 2.9), то вследствие сложения векторов линейная скорость V1 в точке А будет больше, чем V2 в точке В (рис. 2.8, а, б)
V1 = Vорб + Vвр; V2 = Vорб – Vвр. (2.11)
Для вращательной части движения при перемещении из т. 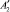 в т. А2 (рис. 2.9) имеет место соотношение
в т. А2 (рис. 2.9) имеет место соотношение
(Vорб + Vвр) – (Vорб – Vвр) = 2Vвр.
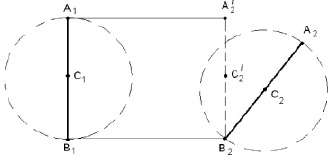
Рис. 2.9. Схема к теореме Шаля
В соответствии с теоремой Шаля схема модели перемещения точек А и В по окружности с радиусом OD показана на рис. 2.10.
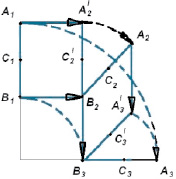
Рис. 2.10. Схема движения шара с диаметром АВ
Из рис. 2.10 видно, что из т. В1 в т. В3 полюс В перемещается поступательно по линейным отрезкам В1В2 и В2В3.
В свою очередь, точка А перемещается из т. А1 в т. А3, имея две составляющие движения: поступательную на линейных отрезках 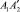 ,
, 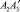 и вращательную – по дугам
и вращательную – по дугам 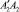 и
и 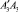 .
.
Это означает, что для т. А в соответствии с принятой моделью вращательная часть движения совершается с радиусом кривизны, равным АВ.
При переходе от движения материальной точки С к движению объемного тела (шар с диаметром АВ, который движется как показано на рис. 2.10), максимальное значение скорости т. А (когда центр масс шара находится в т. D на рис. 2.7) определяется по соотношению
Vmax = Vабс = Vx = Vорб + 2Vвр, (2.12)
а минимальная скорость будет определяться положением полюса в точке В2 и равна нулю Vmin = 0 (рис. 2.10).
Необходимо отметить, что все точки, принадлежащие окружности с диаметром АВ при сложном движении, проходят через экстремальные точки А и В.
Результатом такого моделирования является средняя по модулю скорость Vабс = const, что не противоречит положению о равномерном движении по окружности.
Тогда скорость V произвольной точки тела на окружности диаметром АВ определяется как среднее значение Vmax и Vmin, т.е. при Vmin = 0
Vср = 0,5(Vорб + 2Vвр). (2.13)
Таким образом, в соответствии с разработанной моделью определен радиус кривизны вращательной части движения шара, равный диаметру АВ. Кроме того, определены экстремальные значения скоростей, которые имеют место на окружности с диаметром АВ.
Экстремальные значения скоростей позволяют найти интеграл функции ускорения (скорости) или в простейшем случае – среднее значение ускорения (скорости) в произвольной точке, принадлежащей поверхности шара с диаметром АВ.
8. Расчетная формула гравитационной постоянной выводится на примере тела, находящегося на поверхности Земли.
В этом случае сила тяжести F определяется в соответствии с законом всемирного тяготения
F = G⋅M⋅m /D2, (2.14)
где D – расстояние до оси вращения (см. рис. 2.8–2.10).
С другой стороны, сила тяжести определяется по второму закону Ньютона
F = ma. (2.15)
Приравнивая (2.1) и (2.2), получим
G(Mm /D2) = ma.
Отсюда гравитационная постоянная G
G = aD2 /M. (2.16)
Соотношение для равноускоренного движения тела к центру вращения (вдоль диаметра Земли D)
a = V 2 /2D. (2.17)
Подставим (2.4) в (2.3), тогда
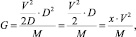
где x = D/2 = R – радиус Земли. С учётом эксцентриситета вращения Земли r = 4,70⋅106 м [72] минимальное расстояние до оси вращения составляет
x = R – r = 6,37⋅106 – 4,70⋅106 = 1,67·106 м.
В результате выведена расчетная формула гравитационной постоянной, которая с учетом V = Vср имеет вид
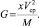 (2.18)
(2.18)
Таким образом, коэффициент G является функцией результирующей скорости орбитального и вращательного движения тела, а также зависит от массы взаимодействующих тел.
Анализ адекватности модели
Адекватность модели подтверждается сравнением результатов расчета с экспериментальными (справочными) данными на следующих примерах.
Пример 1
Рассматривается движение планеты Земля вокруг Солнца в инерциальной гелиоцентрической системе координат XOY из точки D в точку Е (рис. 2.7) с дополнительными допущениями.
1. Рассматривается движение по окружности с радиусом OD (рис. 2.7).
2. Тело движется плоскопараллельно из т. D в т. E по эквипотенциальной траектории, т.е. в однородном поле гравитации.
3. На Землю действует центростремительная сила, т.е. имеет место соотношение (2.10).
Тогда в соответствии с разработанной моделью поступательного движения вращающегося тела центростремительное ускорение на поверхности Земли определяется по соотношению (2.10) с учетом (2.13) и результат расчета принимает вид
aср = (0,5(Vорб + 2Vвр))2 /2D = (0,5(30⋅103 + 2⋅0,8⋅103))2 /2⋅12,744⋅103 = 9,79 м/с2, (2.19)
где D = 2R = 12,744⋅103 км (R – средний радиус Земли); Vорб = 30 км/с; Vвр = 0,8 км/с.
Справочное значение ускорения силы тяжести 9,80 м/с2. Расхождение определения ускорения силы тяжести по сравнению со справочным значением [76] составляет –0,15 %.
Гравитационная постоянная G [77]
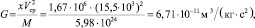 (2.20)
(2.20)
где M – масса Земли.
Справочное значение гравитационной постоянной 6,67⋅10–11 Нм2 /кг2 [71, 76]. Размерность м3/(кг⋅с2) тождественна Нм2 /кг2. Расхождение определения гравитационной постоянной по сравнению со справочной величиной составляет –1 %.
Пример 2
Рассматривается движение Луны вокруг Земли в той же системе координат.
В соответствии с разработанной моделью центростремительное ускорение на поверхности Луны определяется по соотношению (2.19)
aср = (0,5(Vорб + 2Vвр))2 /2D = (0,5(1⋅103 + 2⋅30⋅103))2 /2⋅384⋅106 = 1,31 м/с2,
где D = 384⋅106 м – среднее расстояние от Луны до Земли; Vорб = 1⋅103 м/с;
Vвр = (4,6 + 30⋅103) ≈ 30⋅103 м/с – экстремальное значение скорости при совпадении вектора скорости вращения Луны с вектором орбитальной скорости Земли.
Ускорение силы тяжести на Луне, определенное по закону Всемирного тяготения, составляет
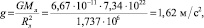
где Mл – масса Луны; Rл – радиус Луны [76]. Расхождение составляет 19 %.
Удовлетворительная сходимость результатов расчета ускорения силы тяжести и гравитационной постоянной с экспериментальными данными подтверждают адекватность модели.
Разработанная модель позволяет объяснить гироскопический эффект (рис. 2.11).
Вследствие совместного переносного и относительного (орбитального и вращательного) движения ротора возникает центростремительная сила, которая обеспечивает устойчивость гироскопа к внешним воздействиям. В частности, не дает ему упасть под действием силы тяжести mg (рис. 2.11).
Ориентация ротора ГТД в соответствии с направлением векторов внешних сил позволяет изменить величину суммарного вектора внешних сил и уменьшить нагрузку на двигатель. Одним из частных случаев реализации предлагаемой модели, применительно к ГТД, является использование ориентации ротора двигателя и летательного аппарата с целью снижения внешних нагрузок. Например, можно расположить летательный аппарат в соответствии с направлением векторов скоростей Vорб, Vвр так, чтобы центростремительное ускорение, возникающее вследствие вращения ротора ГТД, было направлено в противоположную сторону ускорения силы тяжести. В результате получим уменьшение величины силы тяжести, действующей на летательный аппарат. Необходимо отметить, что величина изменения веса серийного двигателя в этом случае составляет порядка нескольких десятков ньютонов, что для серийных изделий пренебрежимо мало.
Результаты расчета коэффициента G1 и ускорения силы тяжести g1 для Земли приведены в табл. 2.1. Величины центростремительной и центробежной сил определяются для тела массой 80 кг.
Из табл. 2.1 видно, в частности, что результаты расчета для Земли удовлетворительно сходятся со справочными данными, что подтверждает адекватность модели. Гравитация проявляется превышением центростремительной силы над центробежной.
Результаты расчета коэффициента G2 и ускорения силы тяжести g2 для Луны приведены в табл. 2.2.
Таблица 2.1
Результаты расчета и справочные данные
|
Обозначение параметра, размерность |
Величина параметра |
Расхождение, % |
|
|
расчетная |
справочная |
||
|
G1, Нм2 /кг2 |
6,71⋅1011 |
6,67⋅1011 |
0,57 |
|
g1, м/с2 |
9,79 |
9,80 |
–0,15 |
|
Fc, Н |
783,3 |
784,0 |
0,4 |
|
Fцб, Н |
1,8 |
– |
– |
Таблица 2.2
Результаты расчета и справочные данные
|
Обозначение параметра, |
Величина параметра |
Расхождение, % |
|
|
расчетная |
справочная |
||
|
G2⋅1011, Нм2 /кг2 |
5,60 |
6,67 |
16 |
|
g2, м/с2 |
1,31 |
1,62 |
19 |
Из табл. 2.2 видно, в частности, что результаты расчета для Луны имеют расхождение 16 и 19 %. Однако, если рассчитать ускорение силы тяжести с учетом расчетного значения коэффициента G2 для Луны, то расхождение снижается с 19 до 3 %.
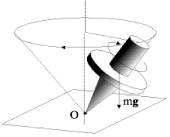
Рис. 2.11. Схема прецессии
гироскопа [78]
Выводы
1. Применение разработанной модели силы тяжести позволяет заложить основу для:
– увеличения подъемной силы летательного аппарата за счет соответствующей ориентации векторов действующих сил;
– объяснения физической сущности гироскопического эффекта;
– объяснения физической сущности самоцентрирования ротора на сверхкритических скоростях вращения.
2. Масса, сосредоточенная в центре вращения, не является причиной притяжения (гравитации), масса есть результат действия центростремительной силы (центростремительного ускорения).
3. Гравитация имеет место при Fc > Fцб. Антигравитация имеет место при Fc < Fцб, то есть определяется соотношением центростремительной и центробежной сил.
