
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.2.9. Предел текучести жаропрочных сплавов
В п. 1.5 показано, что предел текучести при растяжении монокристалла рассчитывается по теоретической формуле, основанной на механизме перемещения краевой дислокации и электростатической природе межатомного взаимодействия t = c/(x/a0)2. Нормальная и тангенциальная проекции напряжения сдвига бездефектного монокристалла связаны известной формулой s = t /(cos α⋅cos b).
Расчетная модель предела текучести для бездефектных монокристаллов является основой для полуэмпирического расчета предела текучести жаропрочных сплавов при высоких температурах. Для этого необходимо иметь ограниченный объем экспериментальных данных для рассматриваемого сплава.
Допущения
1. Температурная зависимость предела текучести основана на зависимости периода кристаллической решетки от температуры.
2. При высоких температурах предел текучести зависит от теплоемкости материала Cp. В частности, в работе [88] показано, что предел текучести зависит от теплоемкости материала при теплосменах.
3. Теоретическая зависимость предела текучести монокристалла (основы сплава) сравнивается с экспериментальной зависимостью для технического металла и совмещается с ней. Для жаропрочных сплавов поступают аналогично.
Расчетные формулы приведены в п. 1.5.
В качестве примера на рис. 2.24 приведена температурная зависимость предела текучести никеля поликристаллического. Точками обозначены экспериментальные (справочные) данные, полученные другими авторами [32, 89, 90], а результаты расчета – сплошными линиями.
На рис. 2.25–2.28 приведены результаты расчета для некоторых сплавов.
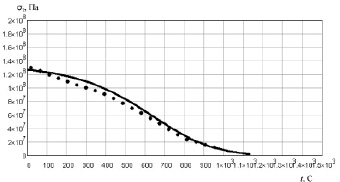
Рис. 2.24. Зависимость предела текучести Ni от температуры:…. – эксперимент [32], ___ – результаты расчета
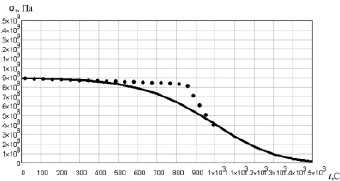
Рис. 2.25. Зависимость предела текучести ЖС6К от температуры:…. – эксперимент [89], ___ – результаты расчета
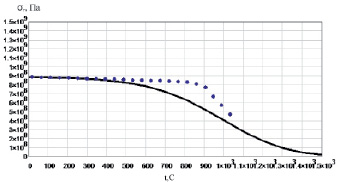
Рис. 2.26. Зависимость предела текучести ЖС6Ф от температуры:…. – эксперимент [89], ___ – результаты расчета
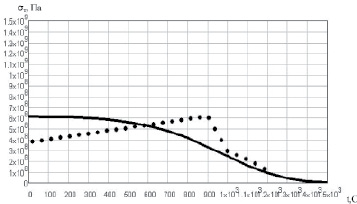
Рис. 2.27. Зависимость предела текучести ВКНА-4 от температуры:…. – эксперимент [90], ___ – результаты расчета
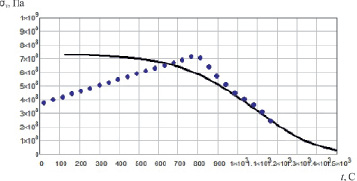
Рис. 2.28. Зависимость предела текучести ВКНА-1В от температуры:…. – эксперимент [90], ___ – результаты расчета
Как видно из графиков, модель хорошо согласуется с результатами эксперимента для кристаллической решетки никеля (рис. 2.24). Для жаропрочных сплавов модель позволяет прогнозировать предел текучести при высоких температурах (рис. 2.25–2.28), когда идет процесс растворения фаз. В этих условиях предел текучести определяется свойствами кристаллической решетки основы сплава.
