Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.2. Особенности кинематики и динамики шламовых смесей в проточной части насоса
При откачке загрязненных шахтных вод (шламовых смесей) проходящая через проточную часть насоса текучая среда является двухфазной: твердые механические частицы с плотностью ρт и вода с плотностью ρ.
Следовательно, на твёрдые частицы и равные им объёмы жидкости при неравенстве плотностей ρт≠ρ будут действовать разные силы, что приведёт к соответствующей разнице и между их кинематическими параметрами (сепарации гидросмеси). Так как подача и напор (давление) насоса определяются в основном кинематикой потока в рабочем колесе, то наличие твёрдого компонента в жидкости приведёт к изменению напорной характеристики, что, в свою очередь, обусловит изменение всех остальных характеристик. Важная особенность гидродинамики двухфазной смеси в проточной части насоса связана с разными физическими свойствами компонентов. При протекании жидкости через рабочее колесо происходит приращение как кинетической, так и потенциальной энергии. Причём последняя у центробежных насосов составляет значительную величину [92]. Твёрдые частицы, обладающие меньшей упругостью, чем жидкость, обладают значительно меньшей аккумулирующей способностью потенциальной энергии. В пределах соблюдения закона Гука удельная энергия упругой деформации [91]
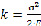, (2.2)
где σ – напряжение в деформируемом теле (давление в жидкости);
Е – модуль упругости.
При равенстве напряжений для компонентов:
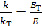(2.3)
где с индексом «T» указаны величины для твердых частиц, без индекса – для жидкости.
Для рассматриваемых условий отношение ЕТ/E ≥ 10. Поэтому твердые частицы при протекании через насос по сравнению с жидкостью приобретают меньшую потенциальную энергию. Вместе с тем, находясь в поле действия тех же сил, что и жидкость, твердые частицы с большей плотностью должны получать и большее приращение кинетической энергии, а следовательно, по существу, обгонять жидкость. У частиц с плотностью ρт<ρ будет обратная картина. При наличии положительной разности в скоростях между твердыми частицами и жидкостью частицы будут передавать часть своей кинетической энергии жидкости. Однако, происходит это в результате силового взаимодействия между компонентами, а не преобразования кинетической энергии частиц в потенциальную, как у жидкости. Объясняется это отсутствием конвективного ускорения у твердых тел. Последнее очень важно при анализе кинематики и динамики компонентов гидросмеси в подводе и отводе насоса.
Движение невязкой жидкости в рабочем колесе описывается уравнением Эйлера [120]:
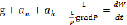(2.4)
где 
, 
,
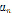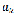– соответственно векторы единичных массовых сил тяжести, переносной и кориолисовой;
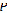– абсолютное давление в жидкости;
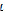– время; 
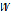– относительная скорость.
На твердую частицу массой pT,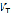 
вследствие наличия градиента давления как по Z, так и по радиусу R, кроме вышеуказанных сил действует также архимедова сила:
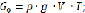(2.5)
и центростремительная:
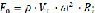(2.6)
где 
– угловая скорость вращения колеса;
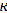– расстояние от оси вращения до центра тяжести частицы.
Из-за наличия градиента давления вдоль оси межлопастного канала на частицу будет действовать гидродинамическая сила
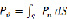(2.7)
где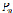
– нормальное напряжение жидкости к поверхности частицы 
.
При движении твердой частицы в невязкой жидкости с ускорением необходимо учитывать присоединенную массу. Для шарообразной частицы диаметром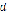 
эта масса
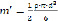(2.8)
С учетом изложенного и данных работ Малеева В. Б. [97] уравнение движения шарообразной твердой частицы в невязкой жидкости, отнесенное к единице массы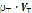 
, будет:
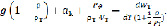(2.9)
Спроектировав слагаемые уравнения (2.8) на направление перемещения частицы ρТ и проинтегрировав в пределах от R1 до R2, получим
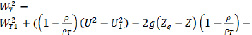
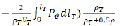(2.10)
где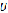 
= ωR – окружная скорость колеса на текущем радиусе.
В уравнении (2.9) индексом 1 отмечены параметры при входе в колесо, без индекса – в произвольной точке колеса.
Решая аналогично уравнение (2.4), получим [71]:
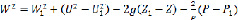(2.11)
Сравним между собой значения скоростей компонентов по уравнениям (2.9) и (2.10). Для перемещаемых в нашем случае твердых материалов их относительная скорость движения в жидкости близка к нулю [92]. Поэтому можно принять, что при входе в колесо насоса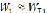 
. При постоянной ширине рабочего колеса 
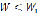. Тогда из уравнения (2.11) имеем:
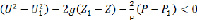(2.12)
Причем, вследствие малости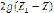 
, как правило,
.
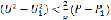В уравнении (2.10) удельная энергия, создаваемая единичной твердой частицей в рабочем колесе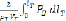 
, как и удельная энергия гравитационных сил 
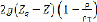, – весьма малые величины. Поэтому определяющим сумму слагаемых, заключенных в квадратных скобках уравнения (2.10), является первое из них. Следовательно, для твердых частиц 
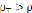[97].
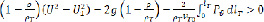(2.13)
Как видно из неравенств (2.11) и (2.12) уравнений (2.10) и (2.11), относительная скорость у частиц с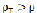
будет большей, чем у жидкости. Для частиц с плотностью 
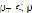неравенство (2.13) будет обратным, а следовательно и 
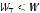. Из приведенного анализа также видно, что разность между скоростями компонентов будет тем большей, чем больше разность их плотностей.
Выполненный анализ позволяет установить полную картину взаимного отношения скоростей между треугольниками скоростей компонентов двухфазной гидросмеси в рабочем колесе насоса. На рис. 2.3, а приведены треугольники скоростей для случая ρт>ρ. Как видно из рисунка, относительная скорость, ее составляющая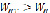 
, угол βТ>β. При этом окружная составляющая абсолютной скорости у твердых частиц меньше, чем у жидкости, т. е. СUT < СU. Естественно, что и угол абсолютной скорости αT > α. По результатам выполненного анализа нетрудно представить и соотношение между треугольниками скоростей компонентов для случая, когда плотность частиц меньше, чем у жидкости (рис. 2.3, б). Треугольники скоростей компонентов полностью определяют траектории их движения в рабочем колесе и в какой-то степени в отводе. Поэтому от них зависит рациональная форма проточной части насоса, а треугольник скоростей твердого компонента, кроме того, определяет и интенсивность абразивного износа проточной части. Треугольники скоростей оказывают также влияние на вид характеристик насоса.
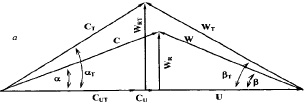
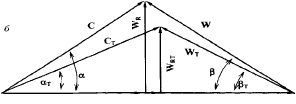
Рис. 2.3. Треугольники скоростей компонентов гидросмеси в рабочем колесе:
а – при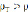 
, б – при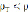 
В межлопастных каналах колеса существуют вихри с направлением вращения противоположным вращению колеса. Угловая скорость вихря пропорциональна подаче. Таким образом, твердые частицы с плотностью ρт>ρ за счет большей относительной скорости, чем у жидкости, подобно лопастям рабочего колеса активно действуют на жидкость и создают в ней приращение напора. Однако вследствие большого профильного сопротивления частиц передача энергии сопровождается значительной диссипацией, что является причиной уменьшения КПД насоса при работе на гидросмеси. Полученные результаты позволяют судить не только о кинематике твердых частиц проточной части, но и о ее износе. Чем больше масса частицы, тем меньше должна быть кривизна траектории ее абсолютного движения в рабочем колесе насоса, тем меньше время ее пребывания в колесе, тем меньше вероятность соприкосновения ее с лицевой стороной лопатки. Наоборот, чем меньше масса частицы, тем больше должна быть кривизна траектории ее абсолютного движения, тем дольше частица находится в колесе, тем вероятнее ее соприкосновение с лицевой стороной лопатки. При одинаковой плотности частиц наиболее мелкие будут перемещаться ближе всего к лицевой поверхности лопатки, наиболее крупные – в наибольшем от нее удалении. Исходя из этого, мелкие частицы будут наиболее интенсивно изнашивать лицевую поверхность лопатки, особенно на выходе из колеса, крупные – на входе в колесо.