
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.3. Инвариантные свойства параллельного проецирования
Геометрические фигуры в общем случае проецируются на плоскость проекций с искажением. Проекции не сохраняют линейные и угловые величины оригинала. Характер искажений зависит от положения геометрической фигуры в пространстве, от аппарата проецирования и от положения плоскости проекций. Однако некоторые геометрические свойства фигур остаются неизменными в процессе проецирования. Такие свойства геометрических фигур называются независимыми или инвариантными для данного аппарата проецирования.
Рассмотрим основные инвариантные свойства параллельного проецирования.
1. Проекция точки есть точка
Это очевидно из самого определения проекции как точка пересечения проецирующей прямой с плоскостью.
2. Проекция прямой есть прямая (рис. 1.6)
Все проецирующие прямые, проходящие через точки прямой а, параллельно направлению проецирования S, образуют проецирующую, или лучевую, плоскость α.
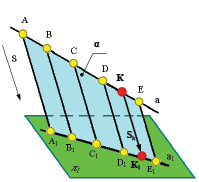
Рис. 1.6. Инвариантные свойства 2, 3, 4
Проекция прямой а на плоскость π1 определяется как линия пересечения этой лучевой плоскости α с плоскостью π1, т. е. прямая.
3. Если точка К принадлежит прямой а, то и проекция этой точки принадлежит проекции прямой (рис. 1.6).
Это свойство следует непосредственно из определения проекции геометрической фигуры как множества проекций всех точек.
Если точка К принадлежит прямой а и плоскости α, то и проецирующий луч SК принадлежит плоскости α. Следовательно, этот луч пересечет плоскость π1 в линии пересечения плоскостей α и π1, т. е. в точке К1, принадлежащей проекции прямой а1.
4. Если точка К делит отрезок АD в отношении m:n то и проекции этой точки делят в таком же отношении проекции этого отрезка (рис. 1.6):
Фигура AEE1A1 – трапеция. Прямая КК1 параллельна боковым сторонам трапеции АА1 и EE1, следовательно делит ее стороны АE и А1E1 на пропорциональные части.
5. Проекция точки пересечения прямых есть точка пересечения проекций этих прямых (рис. 1.7). Действительно, точка К принадлежит одновременно прямым АВ и CD. По третьему инвариантному свойству проекция этой точки К1 должна принадлежать проекциям этих прямых, т. е. должна являться точкой пересечения этих проекций.
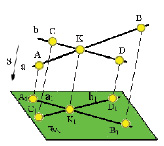
Рис. 1.7. Пример инвариантного свойства 5
6. Проекции параллельных прямых параллельны (рис. 1.8)
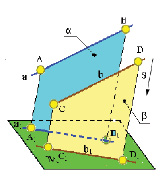
Рис. 1.8. Пример инвариантного свойства 6
Лучевые плоскости α и β, проходят через параллельные прямые АВ и CD. Они параллельны, так как две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости (АВ║CD и АА║СС1). Но две параллельные плоскости пересекаются с третьей по параллельным прямым, следовательно, А1В1║С1D1.
7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.
Исключение составляет многоугольник (плоская ломаная или кривая линия) расположенный в проецирующей (лучевой) плоскости. Такой многоугольник проецируется в прямую линию (рис. 1. 9).
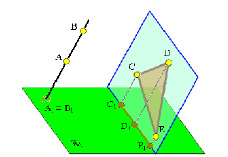
Рис. 1.9. Примеры инвариантных свойств 7, 8
8. Прямая, параллельная направлению проецирования, проецируется на плоскость в точку (рис. 1.9)
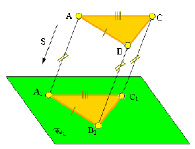
9. Проекция плоской фигуры, параллельной плоскости проекций, конгруэнтна этой фигуре (рис. 1.10).
Две фигуры называются конгруэнтными, или равными, если существует изометрия плоскости, которая переводит фигуры одну в другую. Например, в евклидовой геометрии две фигуры называются конгруэнтными, если одна из них может быть переведена в другую сдвигом, вращением и зеркальным отображением.
Следствия этого инвариантного свойства следующие:
1. Проекция отрезка прямой, параллельной плоскости проекций, конгруэнтна и параллельна самому отрезку (рис. 1.10):
2. Проекция угла, стороны которого параллельны плоскости проекций, конгруэнтна этому углу (рис. 1.10).
 .
.
Рис. 1.10. Пример инвариантного свойства 9 и его следствий
