Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
1.4. Ортогональное проецирование
Ортогональное проецирование является частным случаем параллельного проецирования, когда направление проецирования (ортогонально) к плоскости проекций S ⊥ π1 (рис. 1.11). В этом случае проекция изображаемого объекта называется ортогональной.
Ортогональное проецирование находит широкое применение в инженерной практике для изображения геометрических фигур на плоскости, т. к. обладает рядом преимуществ перед центральным и параллельным (косоугольным) проецированием к которым можно отнести:
а) простоту графических построений для определения ортогональных проекций точек;
б) возможность при определенных условиях сохранить на проекциях форму и размеры проецируемой фигуры.
Указанные преимущества обеспечили широкое применение ортогонального проецирования в технике, в частности для составления машиностроительных чертежей.
Для ортогонального проецирования справедливы все девять инвариантных свойств параллельного проецирования, рассмотренных выше. Кроме того, необходимо отметить еще одно, десятое, инвариантное свойство, которое справедливо только для ортогонального проецирования.
10. Если хотя бы одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость проекций прямой угол проецируется без искажения (рис. 1.11).
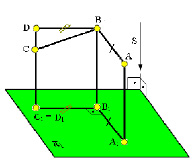
Рис. 1.11. Ортогональная проекция прямого угла
На рис. 1.11 показан прямой угол АВD, обе стороны которого параллельны плоскости проекций π1. По инвариантному свойству 9 этот угол проецируется на плоскость π1 без искажения, т. е.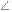 
А1В1D1=90°.
Возьмем на проецирующем луче DD1 произвольную точку С, тогда полученный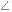 
АВС будет прямым, т. к. АВ ⊥ ВВ1DD1.
Проекцией этого прямого угла АВС, у которого только одна сторона АВ параллельна плоскости проекций π1, будет прямой угол А1В1D1.