Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Краткий курс начертательной геометрии

Пиралова О. Ф., Ведякин Ф Ф.,

1.5. Система трех плоскостей проекций. Эпюр монжа

Все пространственные геометрические фигуры могут быть ориентированы относительно декартовой прямоугольной системы координатных осей – системы трех взаимно перпендикулярных координатных плоскостей (рис. 1.12).

Эти координатные плоскости обозначаются:

1. Горизонтальная плоскость проекций – π1;

2. Фронтальная плоскость проекций – π2;

3. Профильная плоскость проекций – π3.

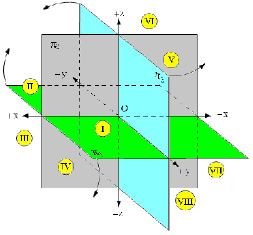
Рис. 1.12. Изображение системы трех плоскостей проекций

Линии пересечения этих плоскостей образуют координатные оси: ось абсцисс – Х; ось ординат – Y; ось аппликат – Z. Точка пересечения координатных осей принимается за начало координат и обозначается буквой О.

Положительными направлениями осей считают: для оси x – влево от начала координат, для оси Y – в сторону зрителя от плоскости π2, для оси z – вверх от плоскости π1; противоположные направления считают отрицательными.

Для упрощения дальнейших рассуждений будем рассматривать только часть пространства, расположенную влево от профильной плоскости проекций π3.

При таком допущении три координатные плоскости проекций образуют четыре пространственных угла – октанта (в общем случае – 8 октантов).

Каждый из октантов представляет часть пространства, в котором располагаются геометрические элементы (точки, прямые, плоскости и поверхности), определяемые соответствующими размерами. Положение этих элементов в пространстве определяется координатами в выбранной системе. Система трёхмерная, поэтому каждая точка пространства имеет три координаты – х,у,z.

Координатой считается кратчайшее расстояние от точки до соответствующей плоскости проекций.

Из рис. 1.12 видно, что ось абсцисс Х делит горизонтальную плоскость проекций π1 на две части: переднюю полу π1 (оси Х и Y) и заднюю полу π1 (оси Х и -Y).

Ось абсцисс Х делит фронтальную плоскость проекций π2 также на две части: верхнюю полу π2 (оси Х и Z) и нижнюю полу π2 (оси Х и -Z).

Оси ординат Y и аппликат Z делят профильную плоскость проекций π3 на четыре части:

1. Верхнюю переднюю полу π3 (оси Y и Z)

2. Верхнюю заднюю полу π3 (оси -Y и Z)

3. Нижнюю переднюю полу π3 (оси Y и -Z)

4. Нижнюю заднюю полу π3 (оси -Y и -Z)

Для того, чтобы получить плоскую (двухмерную) модель пространственных координатных плоскостей проекций, горизонтальную π1 и профильную π3 плоскости совмещают с фронтальной π2 в том порядке как это показано стрелками на рис. 1.12.

При этом горизонтальная плоскость проекций π1 вращается вокруг оси Х на 90°, а профильная плоскость проекций π3 вращается вокруг оси Z также на 90° (направление вращения показано на рис. 1.12).

Полученное таким образом совмещение трех плоскостей проекций (рис. 1.13) является плоской моделью системы трех пространственных координатных плоскостей.

Для построения плоской модели пространственной геометрической фигуры каждая ее точка проецируется ортогонально на плоскости проекций π1, π2 и π3, которые затем совмещаются в одну плоскость. Полученная таким образом плоская модель пространственной геометрической фигуры называется эпюром[2] Монжа или комплексным чертежом Монжа [1,2,5].

Обычно, такая модель даёт три проекции: фронтальную, горизонтальную и профильную.

Порядок построения эпюра точки,
расположенной в первом октанте.

На рис. 1.13 изображена пространственная точка А, координаты которой (x, y, z) показывают величины расстояний, на которые точка удалена от плоскостей проекций.

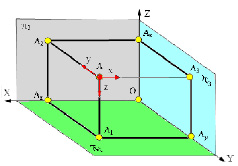
Рис. 1.13. Пространственная модель точки А

Для того чтобы получить ортогональные проекции точки А, необходимо из этой точки опустить перпендикуляры на плоскости проекций.

Точки пересечения этих перпендикуляров с плоскостями проекций образуют проекции точки А:

А1 – горизонтальную проекцию точки;

А2 – фронтальную проекцию точки;

А3 – профильную проекцию точки.

На рис. 1.14 плоскости проекций π1 и π3 совмещены с плоскостью чертежа (с плоскостью проекции π2), а вместе с ними совмещены с плоскостью чертежа и проекции точки А (А1, А2, А3) и, таким образом, получена плоскостная модель координатных плоскостей проекций и плоскостная модель пространственной точки А – её эпюр. Положение проекций точки А на эпюре однозначно определяется ее тремя координатами (рис. 1.14).

На рис. 1.13 и рис. 1.14 также видно, что на эпюре горизонтальная и фронтальная проекции точки лежат на одном перпендикуляре к оси Х, а также фронтальная и профильная проекции – на одном перпендикуляре к оси Z:

А1А2 ⊥ Х, А2А3 ⊥ Z.

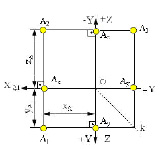
Рис. 1.14. Эпюр точки А

Из рис. 1.12 видно, что точки, расположенные в различных октантах, имеют определенные знаки координат.

В таблице приведены знаки координат точек, расположенных в различных октантах.

Таблица знаков координат

Вопросы для самоконтроля

1. В чём заключается идея метода проецирования?

2. В чём сущность построения эпюра точки?

3. В чём сущность центрального проецирования?

4. Каковы основные свойства центрального проецирования?

5. В чём сущность параллельного проецирования?

6. Каковы основные свойства параллельного проецирования?

7. В чём сущность ортогонального проецирования?

8. Каковы основные свойства ортогонального проецирования?

9. Какие координаты точки однозначно определяют ее положение в пространстве?

10. Как формулируется теорема о проецировании прямого угла?

11. Чем однозначно определяется положение проекций точки на эпюре?

12. Как выполняется построение плоской модели пространственной геометрической фигуры?

13. Как можно построить профильную проекцию точки?

14. Какие координаты точки однозначно определяют ее положение в пространстве?

15. Сколько необходимо иметь проекций точки для определения её положения в пространстве?