
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.2. Прямая. Свойства прямой линии на комплексно мчертеже
Положение в пространстве любой прямой линии однозначно может быть определено заданием двух её точек. Комплексный чертеж прямой может быть представлен в виде комплексного чертежа двух точек прямой (рис. 2.1.б-в). Ещё комплексный чертёж прямой может быть представлен двумя проекциями прямой (рис. 2.1. а).
а б в
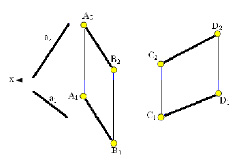
Рис. 2.1. Прямые общего положения
Во всех этих случаях при реконструкции в пространстве прямая линия определяется однозначно и имеет следующие основные свойства:
1. Для деления данного отрезка в данном отношении достаточно разделить в этом отношении одну из проекций данного отрезка, а затем спроецировать делящую точку на другую проекцию отрезка.
Прямая а1 – горизонтальная проекция прямой а на горизонтальную плоскость проекций π1 (а1 ∩ π1).
Прямая а2 – фронтальная проекция прямой а на фронтальную плоскость проекций π2 (а2 ∩ π2).
Прямая а3 – профильная проекция прямой а на профильную плоскость проекций π3 (а3 ∩ π3).
2. Если точка принадлежит прямой, то все её проекции принадлежат проекциям прямой.
3. Если прямая не параллельна и не перпендикуляра ни одной из плоскостей проекций, её называют прямой общего положения (рис. 2.1.).
4. В отличие от прямых частного положения, любой отрезок прямой общего положения проецируется на основные плоскости проекций с искажением своей истинной величины.
