
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
2.3. Положение прямой относительно плоскостей проекций. Частные положения прямой линии
Основываясь на свойствах прямой линии(3 и 4), описанных в п.2.2, следует отметить, что особый интерес в начертательной геометрии представляют прямые частного положения. К прямым частного положения относятся прямые, расположенные определенным образом относительно плоскостей проекций: параллельные, перпендикулярные и принадлежащие плоскостям проекций.
Линии, параллельные плоскостям проекций называются линиями уровня. Рассмотрим изображения на эпюре и отметим основные свойства этих прямых.
Прямые, параллельные плоскостям проекций.
а) горизонтальная прямая h (рис. 2.2) – горизонталь.
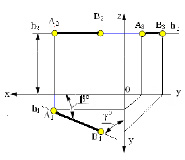
Рис. 2.2. Горизонтальная прямая
Горизонтальная прямая – это прямая, параллельная горизонтальной плоскости проекций π1. Так как все точки этой прямой равноудалены от плоскости проекций π1 (координаты Z всех точек прямой одинаковы), то фронтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Y. На плоскость проекций π1 проецируются без искажения отрезок прямой АВ (А1В1 = АВ) и углы наклона прямой к плоскостям проекций π2 и π3 (углы β0 и γ0).
б) фронтальная прямая f (рис. 2.3) – фронталь.
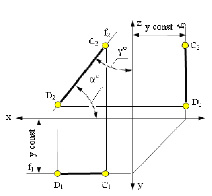
Рис. 2.3. Изображение фронтальной прямой
Фронтальная прямая – это прямая, параллельная фронтальной плоскости проекций π2. Так как все точки этой прямой равноудалены от плоскости проекций π2 (координаты Y всех точек прямой одинаковы), то горизонтальная и профильная проекции прямой соответственно параллельны координатным осям Х и Z. На плоскость проекций π2 проецируются без искажений отрезок этой прямой CD (C2D2 = CD) и углы наклона прямой к плоскостям проекций π1 и π3 (углы α° и γ°).
в) профильная прямая p (рис. 2.4)
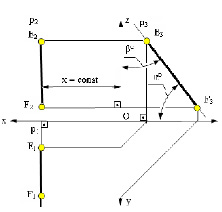
Профильная прямая – это прямая, параллельная профильной плоскости проекций π3 . Так как все точки этой прямой равноудалены от плоскости проекций π3 (координаты Х всех точек прямой одинаковы), то горизонтальная и фронтальная проекции прямой соответственно параллельны координатным осям Y и Z. На плоскость проекций π3 проецируется без искажения отрезок этой прямой EF (E3F3 = EF) и углы наклона прямой к плоскостям проекций π1 и π2 (углы α° и β°).
Кроме прямых линий, рассмотренных выше, на комплексном чертеже, также, изображают прямые, принадлежащие плоскостям проекций. Такие прямые представляют частные случаи горизонтальных, фронтальных и профильных прямых. Характерным признаком, таких прямых на чертеже, является принадлежность одной из проекций этих прямых соответствующей оси.
 .
.
Рис. 2.4. Изображение профильной прямой
Прямые, принадлежащие плоскостям проекций
На рис. 2.5 изображена прямая АВ, которая принадлежит горизонтальной плоскости проекций АВ ⊂ π1 (частный случай горизонтальной прямой Z=0), а фронтальная проекция этой прямой А2В2 принадлежит оси х (А2В2 ⊂ X). При этом, на рисунке показаны углы наклона прямой АВ к фронтальной (β°) и профильной (γ°) плоскостям проекций.
На рис. 2.6. показана прямая, принадлежащая фронтальной плоскости проекций (частный случай фронтальной прямой Y=0), а на рис. 2.7 – профильной плоскости проекций (частный случай профильной прямой Х=0) соответственно.
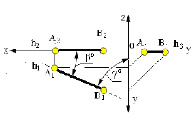
Рис. 2.5. Изображение прямой, принадлежащей горизонтальной плоскости проекций
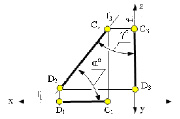
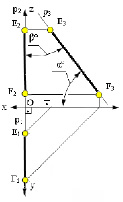
Рис. 2.6. Изображение прямой, принадлежащей фронтальной плоскости проекций
Рис. 2.7. Изображение прямой, принадлежащей профильной плоскости проекций
Прямые линии, перпендикулярные плоскостям проекций.Проецирующие прямые
Прямую, параллельную направлению проецирования и перпендикулярные соответствующим плоскостям проекций называют проецирующей. При прямоугольном проецировании проецирующая прямая параллельна двум плоскостям проекций и перпендикулярна одной.
Если прямая перпендикулярна горизонтальной плоскости проекций, то она называется горизонтально-проецирующей и все её точки проецируются на эту плоскость в точку.
На рис. 2.8 представлена, прямая, перпендикулярная горизонтальной плоскости проекций.
В этом случае во фронтальной плоскости проекцийπ2 проекция прямой А2В2 перпендикулярна оси Х, в профильной плоскости проекций π3, А3В3 – параллельна оси Z, а в горизонтальной плоскости проекций А1 ≡ В1.
Рассматриваемая прямая расположена в первом октанте и все координаты прямой положительные
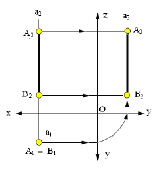
Рис. 2.8. Изображение прямой линии (горизонтально-проецирующей), перпендикулярной горизонтальной плоскости проекций
На рис. 2.9 изображена, прямая, перпендикулярная фронтальной плоскости проекций.
В этом случае в горизонтальной плоскости проекций С1D1 перпендикулярна оси Х, в профильной плоскости проекций С3D3 – параллельна оси Y, а во фронтальной плоскости проекций C2 ≡ D2.
Прямая линия, перпендикулярная фронтальной плоскости проекций называется фронтально-проецирующей прямой и она проецируется на плоскость π2 в точку, а ее горизонтальная проекция перпендикулярна оси Х (рис. 2.9).
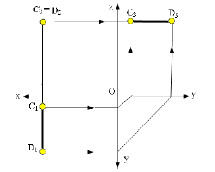
Рис. 2.9. Изображение прямой линии (фронтально-проецирующей),перпендикулярной фронтальной плоскости проекций
Прямая линия, перпендикулярная профильной плоскости (рис. 2.10) проекций называется профильно-проецирующей.
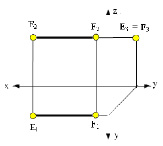
Рис. 2.10. Изображение прямой линии перпендикулярной профильной плоскости (профильно-проецирующей) проекций
Эта прямая проецируется на плоскость π3 в точку, а ее фронтальная проекция E2F2 перпендикулярна оси Z.
Рассмотренные прямые, являются частными случаями фронтальной и горизонтальной прямых соответственно.
