Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Краткий курс начертательной геометрии

Пиралова О. Ф., Ведякин Ф Ф.,

2.5. Плоскость. Способы задания плоскости на комплексном чертеже

Плоскость, простейшая поверхность [5]. Понятие плоскость (подобно точке и прямой) принадлежит к основным понятиям геометрии. Плоскость обладает свойством, что любая прямая, соединяющая две точки плоскости, принадлежит плоскости.

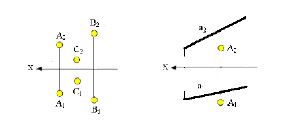
Плоскость на комплексном чертеже однозначно могут определить три точки не расположенные на одной прямой (рис. 2.12 а), прямая и точка, не принадлежащая ей (рис. 2.12 б).

a б

Рис. 2.12. Изображение плоскости, заданной: а – тремя точками; б – точкой и прямой линией

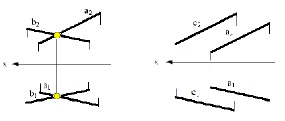
Плоскость на комплексном чертеже можно задать двумя пересекающимися прямыми (рис. 2.13 а) или двумя параллельными прямыми (рис. 2.13 б).

а б

Рис. 2.13.Изображение плоскости, заданной: а – двумя пересекающимися прямыми; б – двумя параллельными прямыми

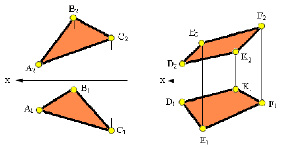
На комплексном чертеже плоскость может быть задана плоской фигурой. На рис. 2.14. а изображён комплексный чертёж, на котором представлена плоскость, заданная плоскостью треугольника. На рис. 2.14 б представлен комплексный чертёж, на котором изображена плоскость, заданная многоугольником.

а б

Рис. 2.14. Изображение плоскости заданной: а – плоскостью треугольника; б – плоскостью многоугольника

В начертательной геометрии существует ещё один способ задания плоскости на комплексном чертеже – следами. Этот способ обладает преимуществом перед другими вариантами ее изображения на эпюре потому, что сохраняется наглядность изображения и требуется указать только две прямые вместо четырех или шести.

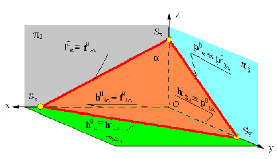
Рис. 2.15. Способ задания плоскости следами плоскости

На рисунке 2.15 показана плоскость общего положения, заданная следами f0, h0, p0, которые расположены, по отношению к плоскостям проекций, под углами, отличными от 90°, но при этом они параллельны соответствующим плоскостям проекций и являются частным случаем изображения линий уровня представленной на рисунке плоскости. Это свойство можно использовать при решении геометрических задач. На рассматриваемом рисунке фронтальный след плоскости α(f0,h0,p0) параллелен фронтальной проекции фронтали этой плоскости f0║f2, горизонтальный след плоскости α(f0,h0,p0) параллелен горизонтальной проекции горизонтали этой плоскости h0║h1,профильный след плоскости α(f0,h0,p0) параллелен профильной проекции профильной прямой этой плоскости p0║p3.