Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Краткий курс начертательной геометрии

Пиралова О. Ф., Ведякин Ф Ф.,

3.4. Взаимное положение прямых

Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны.

1. Пересекающиеся прямые

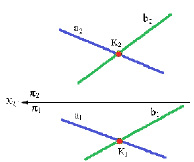
Пересекающимися прямыми называются, такие, прямые, которые имеют одну общую точку. На комплексном чертеже проекции точки пересечения прямых находятся на одной линии связи.

Из инвариантного свойства 5 следует, что проекция точки пересечения проекций прямых а и b есть точка пересечения этих прямых (рис. 3.4).

.

Рис. 3.4. Изображение пересекающихся прямых

2. Параллельные прямые

На рис. 3.5 изображены проекции параллельных прямых а и b, пересекающихся в несобственной точке (прямых, лежащих в одной плоскости и пересекающихся в бесконечно удаленной точке).

Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны.

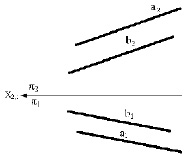
Рис. 3.5. Изображение параллельных прямых

3. Скрещивающиеся прямые

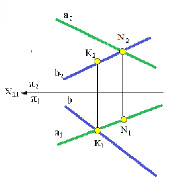
Скрещивающиеся прямые – это прямые лежащие в разных плоскостях и не имеющие ни одной общей точки. На комплексном чертеже (рис. 3.6) точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси Х (в отличие от пересекающихся прямых, см. рис. 3.4).

.

Рис. 3.6. Изображение скрещивающихся прямых