
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
3.5. Прямая и точка на плоскости
Прямая a принадлежит плоскости α, если две ее точки А и В принадлежат этой плоскости α (ΔКLM). Справедливо и обратное утверждение: если точки А и В принадлежат плоскости α (ΔКLM), то прямая а, проходящая через эти точки, принадлежит плоскости α(рис. 3.7, а).
Прямые a и m, принадлежащие разным плоскостям показаны на рис. 3. 7. Прямая a принадлежит плоской фигуре LKM, потому что на проекциях прямой и плоской фигуры имеются две общих точки А и В. Прямая m принадлежит плоскости, заданной параллельными прямыми c и d, т. к. она проходит через точки С и D, расположенные на этих прямых.
Прямая принадлежит плоскости, если ее следы принадлежат одновременно следам плоскости.
Справедливо и обратное утверждение: если следы прямой принадлежат следам плоскости, то эта прямая принадлежит плоскости.
Кроме того, существует еще одно свойство, определяющее взаимное положение точки и плоскости: точка принадлежит плоскости, если она расположена на прямой, принадлежащей этой плоскости (рис. 3.7)
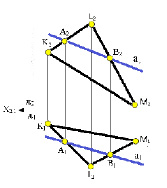
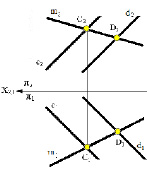
а б
Рис. 3.7. Изображение прямой m, принадлежащей плоскости
