Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Краткий курс начертательной геометрии

Пиралова О. Ф., Ведякин Ф Ф.,

3.6. Взаимное положение прямой и плоскости

Существует несколько положений прямой относительно плоскости.

1. Прямая расположена в плоскости.

2. Прямая параллельна плоскости.

3. Прямая пересекает плоскость.

а) прямая параллельная плоскости (рис. 3.8).

Рассмотрим признак параллельности прямой и плоскости. Прямая параллельна плоскости, когда она параллельна любой прямой, лежащей в этой плоскости.

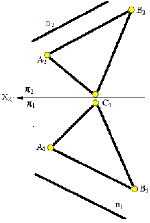
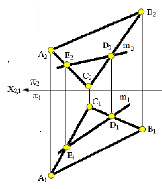
Прямая m параллельна плоскости α(ΔABC), так как она расположена в плоскости (рис. 3.8. б) и имеет признак принадлежности плоскости – две общих точки (D,E), прямая n (рис. 3.8. а) параллельна плоскости α(ΔABC), потому, что она параллельна прямой AB, которая принадлежит этой плоскости.

а б

Рис. 3.8. Прямые, параллельные плоскостям треугольников АВС:а – прямая n находится вне плоскости; б – прямая m находится в плоскости

б. Прямая перпендикулярная плоскости.

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. Подробно перпендикулярность прямых рассмотрена в разделе 4.