
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.1. Условие перпендикулярности двух прямых на комплексном чертеже
Особый интерес с точки зрения решения задач начертательной геометрии представляют перпендикулярные прямые.
Из классической Евклидовой геометрии известно следующее свойство перпендикулярности двух прямых:
Две прямые перпендикулярны, если угол между ними составляет 90°.
Кроме того, в начертательной геометрии существует еще одно утверждение на эту тему:
Две прямые перпендикулярны, если одна из них линия уровня.
Для подтверждения этого заключения рассмотрим примеры, приведенные на рис. 4.1. Предположим что необходимо через точку А провести прямую  , пересекающую горизонталь h под прямым углом
, пересекающую горизонталь h под прямым углом 
 h (рис. 4.1. а).
h (рис. 4.1. а).
Так как одна из сторон h прямого угла параллельна плоскости π1, то на эту плоскость прямой угол спроецируется без искажения. Поэтому через горизонтальную проекцию точки А1проведем горизонтальную проекцию искомой прямой  1. Отметим горизонтальную проекцию точки пересечения прямой и горизонтали М1=
1. Отметим горизонтальную проекцию точки пересечения прямой и горизонтали М1=  1 ∩ h1. Найдем по принадлежности фронтальную проекцию точки пересечения М2. Точки А2 и М2 определяют фронтальную проекцию искомой прямой
1 ∩ h1. Найдем по принадлежности фронтальную проекцию точки пересечения М2. Точки А2 и М2 определяют фронтальную проекцию искомой прямой  . Две проекции прямой определяют ее положение в пространстве.
. Две проекции прямой определяют ее положение в пространстве.
Если вместо горизонтали будет задана фронталь f, то геометрические построения по проведению прямой 
 f аналогичны рассмотренным с той лишь разницей, что построения неискаженной проекции прямого угла следует начинать с фронтальной проекции (рис. 4.1. б).
f аналогичны рассмотренным с той лишь разницей, что построения неискаженной проекции прямого угла следует начинать с фронтальной проекции (рис. 4.1. б).
На основании теоремы, обратной теореме о проецировании прямого угла, можно решить на комплексном чертеже обратную задачу: можно по заданному на комплексном чертеже изображению углов с вершинами М (рис. 4.1) определить, что в действительности они равны 90°. Если, например, рассмотрим угол с вершиной М (рис. 4.1.а), то, очевидно, что h || π1; ℓ1∩ h1= 90°, а следовательно, ℓ ∩ h = 90°.
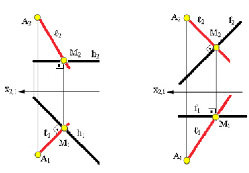
а б
Рис. 4.1. Примеры построения на комплексном чертеже перпендикулярных прямых: а – 
 h; б –
h; б – 
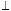 f
f
