
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.4. Свойства перпендикулярных плоскостей
Если плоскость проходит через перпендикуляр к другой плоскости, то заданная плоскость перпендикулярна второй плоскости.
Если две плоскости взаимно перпендикулярны, то прямая, проведенная в одной плоскости перпендикулярно линии пересечения плоскостей, перпендикулярна другой плоскости.
На рис. 4.4 изображены две проецирующие плоскости β, γ и произвольная плоскость δ, следы которой проходят через следы прямой а.
На рис. 4.5 изображён комплексный чертёж, на котором представлены две взаимно-перпендикулярные плоскости.
Это плоскость, заданная фигурой треугольника ∆АВС и плоскость, заданная пересекающимися прямыми КМ и КN. Их перпендикулярность подтверждает прямая b, перпендикулярная плоскости Δ АВС, потому, что её проекции перпендикулярны соответствующим проекциям линий уровня плоскости Δ АВС. Проекции линий уровня плоскости Δ АВС выполняют условия перпендикулярности прямой b и плоскости, потому, что b1 ⊥ h1, а b2 ⊥ f2.
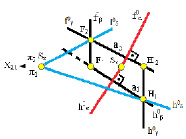
Рис. 4.4. Условие перпендикулярности плоскостей
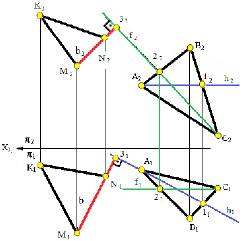
Рис. 4.5. Изображение двух взаимно-перпендикулярных плоскостей
По условию перпендикулярности, любая плоскость (например, плоскость, заданная двумя пересекающимися прямыми КМ и КN), проходящая через прямую b, перпендикулярную плоскости Δ АВС, перпендикулярна плоскости Δ АВС.
