
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
4.6. Линия наибольшего наклона (ската)
К группе главных линий плоскости относится прямая, принадлежащая плоскости и перпендикулярная линиям уровня этой плоскости – горизонтали, фронтали или профильной прямой и (или) соответствующим следам плоскости. Эта линия получила название линии наибольшего наклона заданной плоскости к плоскостям проекций П1, П2, П3. Иногда линию наибольшего наклона к плоскости называют линией ската.
Следует иметь ввиду, что линия наибольшего наклона может использоваться для определения угла наклона заданной плоскости к плоскостям проекций.
Если рассматривать такую линию ℓ в пространстве (рис. 4.9), то можно сделать вывод о том, что линия наибольшего наклона ℓ и ее горизонтальная проекция ℓ1 образуют линейный угол MNM1 (MN ⊥ h0 и M1N ⊥ h0), который служит мерой двугранного угла, составленного горизонтальной и заданной плоскостями.
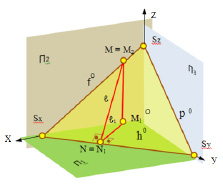
Рис. 4.9. Изображение линии наибольшего наклона плоскости
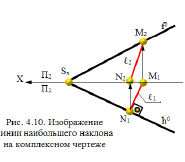
На комплексном чертеже в двух плоскостях проекций (рис. 4.10) изображение линии наибольшего наклона изображается с учётом двух её проекций ℓ (ℓ1,ℓ2).
На комплексном чертеже для линии наибольшего наклона заданной плоскости к горизонтальной плоскости проекций характерно, что её горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали h этой плоскости.
При наклоне к фронтальной плоскости проекций, фронтальная проекция линии наибольшего наклона перпендикулярна к фронтальной проекции фронтали f этой плоскости и, наконец, профильная проекция линии наибольшего наклона плоскости к профильной плоскости проекций займет положение, перпендикулярное к профильной проекции профильной прямой p.
Рассмотрим (рис. 4.11) пример построения линии наибольшего наклона (ЛНН) ℓ плоскости α (a || b) к горизонтальной плоскости проекций П1.
Построение линии наибольшего наклона плоскости ℓ на комплексном чертеже начинается с построения её горизонтальной проекции ℓ1.
На рисунке показана линия наибольшего наклона плоскости α (a ║ b) к горизонтальной плоскости проекций П1 – прямая ℓ.
Рассмотрим алгоритм нахождения линии наибольшего наклона плоскости α(a ║ b) к одной из плоскостей проекций на комплексном чертеже.
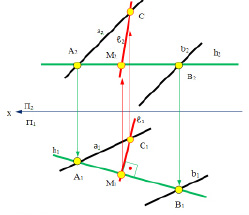
Рис. 4.11. Изображение линии наибольшего наклона плоскости α (a ║ b)
к горизонтальной плоскости проекций П1
Прежде чем провести горизонтальную проекцию ℓ1, определяем направление горизонтальной проекции горизонтали h1:
- проводим произвольную фронтальную проекцию h2(h2║x);
- отмечаем точки A2=h2∩a2 и B2=h2∩b2;
- по A2 и B2 находим A1 и B1, которые определяют положение h1.
Далее:
- через произвольную точку С1 плоскости α проводим ℓ1 (ℓ ⊥ h1);
- отмечаем M1 = ℓ1∩ h1;
- по С1 и M1 находим С2 и M2;
- соединив эти две точки, определим положение фронтальной проекции прямой ℓ2 – линии наибольшего наклона плоскости α (a ║ b) к горизонтальной плоскости проекций П1.
Обращаясь к рис. 4.9. можно сделать вывод, что для определения углов α° и β° наклона плоскости a ║ b к горизонтальной П1 и фронтальной П2 плоскостям проекции линия наибольшего наклона плоскости должна быть построена в этой плоскости дважды – к горизонтали этой плоскости h и фронтали f.
Из рисунка видно, что угол наклона α° определяется из прямоугольного треугольника МNM1, в котором гипотенуза MN является натуральной величиной линии наибольшего наклона плоскости, а угол α° является углом между натуральной величиной ℓ и её проекцией ℓ1 на горизонтальной плоскости проекций П1. Следовательно, при определении угла наклона плоскости α (a ║ b) на комплексном чертеже необходимо после построений (рис. 4.11), определивших направление линии наибольшего наклона к П1, определить натуральную величину известного отрезка М1С1 (рис. 4.12).
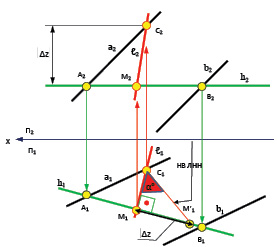
Рис. 4.12. Определение угла наклона плоскости
к горизонтальной плоскости проекций
Для этого необходимо воспользоваться правилом прямоугольного треугольника и построить прямоугольный треугольник на двух катетах, один из которых – это отрезок М1С1, а величину второго катета Δz определить во фронтальной плоскости проекций П2 как разницу начала и конца отрезка М2С2. Величину Δz отложить под прямым углом к М1С1 и получить точку М’1, которую соединить с точкой С1. Линия М’1С1 – натуральная величина отрезка М1С1 = ℓ1. Значит найдена натуральная величина линии наибольшего наклона заданной плоскости (НВ ЛНН) к горизонтальной плоскости проекций П1. Согласно правилу прямоугольного треугольника известно, что в построенном прямоугольном треугольнике угол между гипотенузой (натуральной величиной отрезка) и проекцией отрезка является углом наклона к плоскости проекций. Значит, в нашем случае (рис. 4.12) получена величина угла наклона (α°) заданной плоскости α (a ║ b) к горизонтальной плоскости проекций П1.
Для определения угла наклона β° заданной плоскости к фронтальной плоскости проекций П2 следует выполнить на комплексном чертеже действия аналогичные действиям при определении α°.
Разница в определении состоит в том, что построение начинается с определения фронтали f заданной плоскости.
Рассмотрим (рис. 4.13) плоскость, заданную двумя параллельными прямыми α (a ║ b) и выполним построения линии наибольшего наклона в заданной плоскости для нахождения угла наклона этой плоскости к фронтальной плоскости проекций П2.
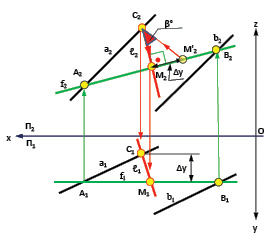
Рис. 4.13. Определение угла наклона плоскости к фронтальной плоскости проекций
Угол α° – это угол наклона прямой ℓ к горизонтальной плоскости проекций П1. Он соответствует углу наклона плоскости α (a ║ b) к той же плоскости проекций П1.
Угол β° – это угол наклона прямой ℓ к фронтальной плоскости проекций П2. Он соответствует углу наклона плоскости α (a ║ b) к той же плоскости проекций П2.
Вопросы для самоконтроля
1. Каковы условия перпендикулярности прямых линий на комплексном чертеже?
2. Каковы условия перпендикулярности прямой к плоскости на комплексном чертеже.
3. Какова сущность способа прямоугольного треугольника?
4. Какое свойство линии наибольшего наклона является основным?
5. Как можно определить действительную величину отрезка, находящегося в общем положении по отношению к плоскостям проекций?
6. Как определяется угол наклона плоскости к плоскостям проекцийс помощью линий наибольшего наклона?
