
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
5.6. Вращение вокруг линии уровня (совмещениес плоскостью уровня)
Если в качестве оси вращения использовать линию уровня, то истинную величину плоской фигуры общего положения можно построить одним поворотом, не выполняя двойного преобразования чертежа, что имело место в замене плоскостей проекций, плоскопараллельном перемещении и вращении вокруг проецирующей прямой. Решение задач вращением геометрических фигур вокруг линии уровня (горизонтали или фронтали) производится с целью совмещения этих фигур с плоскостью уровня. На этом способе основано построение разверток цилиндрических и призматических поверхностей способом раскатки.
Рассмотрим на рис. 5.22 пример вращения точки B вокруг горизонтали h.
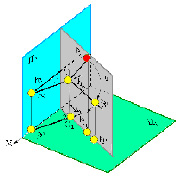
Рис. 5.22. Пример вращения точки В вокруг горизонтали h
Точка В, при вращении вокруг горизонтальной линии уровня h, перемещается по окружности, плоскость которой (α) перпендикулярна к линии уровня h и, соответственно, α1 ⊥ h1. Точка В описывает окружность радиусом ОВ и проецируется на горизонтальную плоскость проекций П1 в виде отрезка прямой, а на П2 в виде эллипса. В рассматриваемом случае ось вращения – горизонталь, следовательно, траектория точки В будет находиться в горизонтально-проецирующей плоскости.
Для того, чтобы на комплексном чертеже переместить точку В путём вращения вокруг линии уровня, нужно знать центр вращения и величину радиуса вращения. Центр вращения известен. Он находится в точке пересечения линии уровня с плоскостью, в которой вращается точка В. Для определения величины радиуса вращения ОВ необходимо воспользоваться способом прямоугольного треугольника (рис. 5.23).
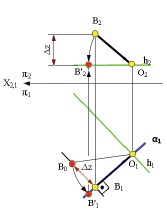
Рис. 5.23. Пример перемещения точки В вокруг горизонтали h
на комплексном чертеже
Для определения натуральной величины радиуса в плоскости П1 необходимо построить прямоугольный треугольник ΔО1В1 В0. Для этого за первый катет принимаем горизонтальную проекцию [O1 В1] радиуса OВ; второй катет равен разности аппликат концов отрезка ОВ |zВ-zВ’|. Гипотенуза треугольника ΔО1В1В0 это O1В0 = R. Новое, после поворота, положение точки В’1 находится в месте пересечения дуги окружности, проведённой из горизонтальной проекции центра вращения O1, радиусом, равным [O1 В0] с горизонтальным следом h0α горизонтально-проецирующей плоскости α в которой вращается точка В. Следующий пример представлен на рис. 5.24.
В этом примере рассмотрено применение способа вращения точки вокруг линии уровня при определении натуральной величины плоскости общего положения.
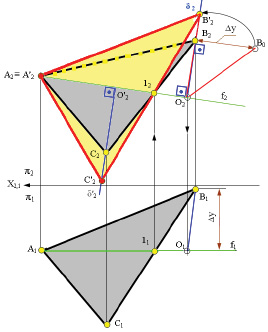
Рис. 5.24. Пример вращения плоскости вокруг фронтали
В этом случае применяется другая линия уровня – фронталь f, которую нужно провести в плоскости. Такая задача решается аналогично предыдущей задаче, но в ней положения точек А и 1 не меняются, потому что через них проходит фронталь, а определить необходимо новые положения точек В и С, вращающихся вокруг фронтали до положения параллельного с фронтальной плоскостью проекций П2.
Вращение плоскости треугольника ΔАВС сводится к вращению только одной ее точки, например вершины В, не принадлежащей оси вращения, так как положение плоскости в пространстве определяется тремя известными точками А, В и 1.
Для определения нового положения точки В, определяется центр её вращения О2. Для этого из точки В2 на фронтальную проекцию фронтали f2 необходимо опустить перпендикуляр, который является радиусом вращения точки В вокруг фронтали, а затем по линии связи определить горизонтальную проекцию центра вращения О1.
Когда в результате вращения точка В окажется в плоскости δ, т. е. параллельной фронтальной плоскости проекций П2, ее фронтальная проекция В2 будет удалена от фронтальной проекции оси вращения f2 на расстояние, равное натуральной величине радиуса вращения точки В.
Натуральную величину радиуса вращения можно определить как гипотенузу В2В0прямоугольного треугольника (см. раздел 4.5), одним катетом которого является фронтальная проекция радиуса В2O2, а вторым – разность координат Δy точек В1 и О1. Для определения нового положения точки В’2, полученную величину, вращением вокруг центра О2 перенести на проекцию плоскости δ2.
Новое положение С’2 вершины С определяется как точка пересечения прямой В’1 с плоскостью δ’, в которой перемещается точка С. Новая фронтальная проекция С’2 точки С2 определится как точка пересечения фронтальной проекции (В2’12) прямой (В’1) с фронтальной проекцией δ’2 плоскости δ.
Треугольник ΔА’В’С’ параллелен П2, следовательно, ΔА2В2С2 ≡ ΔABC.
Вопросы для самоконтроля
1. Какие способы преобразования чертежей используют в курсе начертательной геометрии?
2. В чём состоит принцип способа замены плоскостей проекций?
3. Как нужно располагать дополнительные плоскости проекций, чтобы прямую общего положения преобразовать в: а) прямую уровня; б) проецирующую прямую.
4. Как нужно располагать дополнительные плоскости проекций, чтобы плоскость общего положения преобразовать в: а) проецирующую; б) плоскость уровня?
5. Как определяется направление плоскости проекций при преобразовании плоскости общего положения в плоскость фронтально-проецирующую?
6. Каков алгоритм решения задачи при определении углов наклона плоскости к плоскостям проекций способом замены плоскостей проекций?
7. Каков алгоритм решения задачи при определении натуральной величины плоскости общего положения способом замены плоскостей проекций?
8. Каков принцип способа вращения вокруг проецирующих прямых линий?
9. Какую прямую принимают за ось вращения при преобразовании плоскости общего положения в горизонтально-проецирующую?
10. Какую прямую принимают за ось вращения при преобразовании плоскости общего положения во фронтально-проецирующую?
11. Каков алгоритм определения натуральной величины плоскости способом плоскопараллельного перемещения?
12. Каков алгоритм определения натуральной величины плоскости способом вращения вокруг прямых, параллельных плоскостям проекций?
13. Какие основные метрические задачи можно решать с помощью дополнительного проецирования?
