
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
6.2. Определение расстояний между геометрическими фигурами
Искомое расстояние во всех задачах этой группы измеряется длиной отрезка, заключенного между заданными геометрическими фигурами и перпендикулярного к одной из них или одновременно к обеим. Этот отрезок проецируется в конгруэнтный ему отрезок на плоскость проекций, которая будет перпендикулярна одной или обеим геометрическим фигурам, между которыми определяется расстояние. Алгоритм решения задач этой группы будет следующим:
1. Одним из способов преобразования комплексного чертежа привести обе заданные геометрические фигуры (или одну из них) в положение, перпендикулярное какой-либо плоскости проекций.
2. Построить проекцию искомого отрезка на эту плоскость.
Выбирая способ преобразования комплексного чертежа при составлении алгоритма, следует учитывать требования к компактности чертежа, четкость и возможную простоту графических операций.
Задача 1 . Определение расстояния от точки М до прямой АВ общего положения (рис. 6.1).
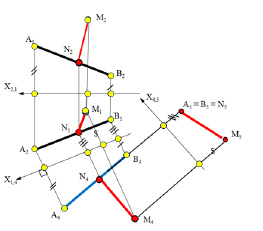
Рис. 6.1. Определение расстояния от точки М до прямой АВ
Искомое расстояние измеряется длиной отрезка /МN/ перпендикуляра, опущенного из точки М на прямую АВ. Отрезок [МN] спроецируется в конгруэнтный ему отрезок на плоскость проекций, перпендикулярную прямой АВ.
Составляем алгоритм решения:
1. Преобразовать прямую АВ в проецирующую прямую способом замены плоскостей проекций.
2. Построить проекцию отрезка [МN] на плоскость П5 ⊥ АВ, длина которого М5N5 определяет искомое расстояние.
Для преобразования прямой линии АВ общего положения в проецирующую линию необходимо выполнить две последовательные замены плоскостей проекций: вначале прямую линию АВ преобразовать в линию уровня.
Для этого проведена замена плоскости проекций П2 на новую плоскость П4, перпендикулярную плоскости П1 и параллельную прямой АВ. Затем линия уровня преобразована в проецирующую прямую, для чего проведена замена плоскости проекций П1 на плоскость П5, в которой построены проекции А5В5 прямой линии АВ и М5N5 искомой линии МN в системе плоскостей проекций П4/П5.
Отрезок [М5N5] является искомым: [М5N5] ≅ [МN] и /М5N5/ = /МN/. На рис. 6.1 показано построение проекций [М4N4], [М1N1] и [М2М2] отрезка [МN] обратным преобразованием.
Задача 2.Определить расстояние между параллельными прямыми а и b (рис. 6.2).
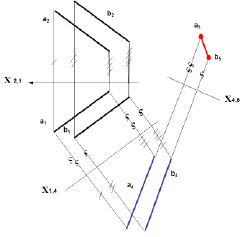
Рис. 6.2. Пример определения расстояния между параллельными прямыми
Для решения задачи необходимо выполнить две замены плоскостей проекций. Вначале прямые a и b необходимо сделать прямыми уровня a4 b4. Для чего плоскость П4 расположить параллельно a1 и b1 для получения натуральной величины a4b4 указанных прямых. Затем, перпендикулярно натуральным величинам прямых, ввести новую плоскость П5 перпендикулярную плоскости П4, в которой расположены прямые.
В этом случае расстояние а5 b5 между ними и будет искомой натуральной величиной расстояния между параллельными прямыми a и b (рис. 6.2).
Задача 3.Определение расстояния от точки до плоскости.
Решение задачи приведено на рис. 6.3.
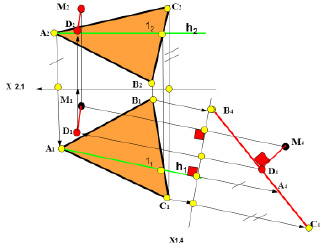
Рис. 6.3. Определение расстояния от точки до плоскости
Примечания: 1) Проекция перпендикуляра М1N1 в П1 располагается параллельно П4, потому что в плоскости П4имеется ее натуральная величина.
2) Задачи 1-3 можно также решать по следующей схеме: вначале определить метрически искаженные проекции искомого отрезка, а затем способом прямоугольного треугольника определить его действительную величину.
Для определения расстояния от точки М до плоскости треугольника ΔАВС необходимо плоскость треугольника общего положения ΔАВС преобразовать в плоскость проецирующую. Для этого нужно произвести замену плоскости проекций П2 на П4 перпендикулярно h1.
Плоскость ΔАВС преобразуется в линию С4А4В4. На эту же плоскость П4 спроецируется точка М (М4). Перпендикуляр из М4 на линию С4А4В4 будет натуральной величиной расстояния от точки М до плоскости Δ АВС. Проекции перпендикуляра переносятся в плоскости проекций П1 и П2 по соответствующим линиям связи, расстояния от точки М до плоскости Δ АВС. Проекции перпендикуляра переносятся в плоскости проекций П1 и П2 по соответствующим линиям связи.
Задача 4. Определить уголφмеждускрещивающимися прямыми m и n. Решение задачи приведено на рис. 6.4.
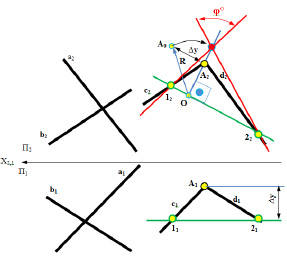
Рис. 6.4. Определение величины угла
между двумя скрещивающимися прямыми линиями
Углом, между скрещивающимися прямыми, является плоский угол, образованный прямыми, параллельно заданным скрещивающимся прямым, проведёнными через любую, выбранную точку.
Для решения поставленной задачи необходимо выполнить следующие графические построения (рис. 6.4):
- построить плоский угол аналогичный искомому. Взяв за вершину угла на свободном месте чертежа точку А, провести прямые с ║ а и d ║ b;
- построить фронталь (или горизонталь) для плоского угла;
- вращением вершины плоского угла вокруг фронтали (или горизонтали) найти его величину φ.
Задача 5. Определить расстояние между скрещивающимися прямыми a и b. Предложенную задачу можно решить с помощью преобразования комплексного чертежа (рис. 6.5).
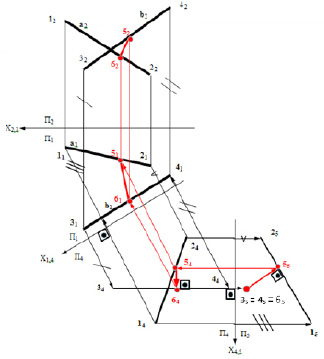
Рис. 6.5. Пример определения расстояния между скрещивающимися прямыми линиями
Для этого необходимо одну прямую (b) преобразовать в проецирующую прямую. Из любой точки (65) этой прямой опустить перпендикуляр на вторую прямую и получить точку (65). Перпендикуляр 5565 окажется кратчайшим расстоянием между скрещивающимися прямыми. Значит искомое расстояние найдено. Для преобразования, заданной прямой b, нужно решить вторую задачу на преобразование подобную задаче, представленной на рис. 5.3.
