
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.1. Понятия и определения
В геометрии и топологии[1] поверхностью называют двумерное топологическое многообразие. Наиболее известными примерами поверхностей являются границы геометрических тел в обычном трёхмерном евклидовом пространстве.
С другой стороны, существуют поверхности (например, бутылка Клейна. Рис. 7.1), которые нельзя вложить в трёхмерное евклидово пространство без привлечения сингулярности или самопересечения.
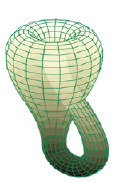
Рис.7.1. Изображение бутылки Клейна
«Двумерность» поверхности подразумевает возможность реализовать на ней метод координат, хотя и необязательно для всех точек. Так, поверхность Земли (в идеале) представляет собой двумерную сферу, широта и долгота каждой точки которой являются её координатами (за исключением полюсов и 180-го меридиана).
Концепция поверхности применяется в физике, инженерном деле, компьютерной графике и прочих областях при изучении физических объектов. Например, при анализе аэродинамических качеств самолёта, который базируется на обтекании поверхности самолёта потоком воздуха.
