Научная электронная библиотека

Монографии, изданные в издательстве Российской Академии Естествознания

Краткий курс начертательной геометрии

Пиралова О. Ф., Ведякин Ф Ф.,

7.2. Способы задания поверхностей

В математике поверхность определяется как множество точек, координаты которых удовлетворяют определённому виду уравнений:

F(x, y, z) = 0 (1)

Если функция F(x, y, z) = 0 непрерывна в некоторой точке и имеет в ней непрерывные частные производные, по крайней мере, одна из которых не обращается в нуль, то в окрестности этой точки поверхность, заданная уравнением (1), будет правильной поверхностью.

Помимо указанного выше неявного способа задания, поверхность может быть определена явно, если одну из переменных, например, z, можно выразить через остальные:

z = ƒ(x, y) (2)

Также существует параметрический способ задания. В этом случае поверхность определяется системой уравнений:

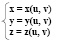(3)