
Научная электронная библиотека
Монографии, изданные в издательстве Российской Академии Естествознания
7.7. Неразвертывающиеся (косые) линейчатые поверхности
Линейчатой поверхностью называется поверхность, образованная при перемещении прямой линии в пространстве по какому-либо закону. Характер движения прямолинейной образующей определяет вид линейчатой поверхности. Обычно закон движения образующей задаётся с помощью направляющих линий. В общем случае для задания линейчатой поверхности необходимы три направляющие линии, которые могут однозначно задать закон перемещения направляющей. Выделим на линейчатой поверхности три какие-нибудь линии a, b и c и примем их за направляющие (рис. 7.17).
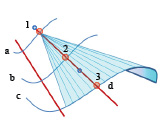
Рис. 7.17. Линейчатая поверхность в общем случае
Изучение группы линейчатых неразвертывающихся поверхностей можно начать с цилиндроидов – поверхностей с плоскостью параллелизма (поверхности Каталана), поверхностей, образуемых движением прямой, скользящей по двум кривым направляющим, не лежащим в одной плоскости, и остающейся все время параллельной, так называемой, плоскости параллелизма (рис.7.18).
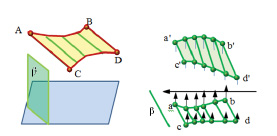
а б
Рис. 7.18. Пример цилиндроида: а – в пространстве; б – на комплексном чертеже
Следующей поверхностью в этой группе является коноид, который представляет собой линейчатую неразвертывающуюся поверхность, которая образуется движением прямой, скользящей по двум направляющим, не лежащим в одной плоскости, и остающейся все время параллельной, так называемой, плоскости параллелизма.
Приэтом нужно знать, что одна из этих направляющих является прямой линией (рис. 7.19).
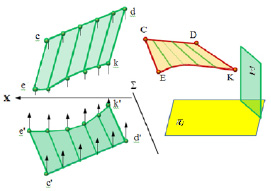
а б
Рис. 7.19. Пример коноида: а – на комплексном чертеже; б – в пространстве
Если же обе направляющие цилиндроида заменить прямыми линиями (скрещивающимися), то образуется линейчатая неразвертывающаяся поверхность с плоскостью параллелизма – косая плоскость, или линейчатый параболоид, или гиперболический параболоид (рис. 7.20).
Своё название (гиперболический параболоид) линейчатая поверхность получила из-за того, что при пересечении ее соответствующими плоскостями в сечении можно получить параболы и гиперболы
Разновидностями косых поверхностей являются линейчатые поверхности с направляющей плоскостью и частные их виды – линейчатые поверхности с плоскостью параллелизма (поверхности Каталана).
В первом случае (рис. 7.20, а) поверхность однозначно задается двумя направляющими прямолинейными скрещивающимися линиями d, n и направляющей плоскостью γ, которая заменяет третью направляющую линию. Образующая прямая скользит по двум направляющим и всё время остаётся параллельной плоскости параллелизма γ.
Если плоскости параллелизма перпендикулярны друг другу γ ⊥ π1 , то гиперболический параболоид называется прямым.
На рис. 7.20, б изображён комплексный чертёж косой плоскости. По своему виду эта поверхность напоминает седло.
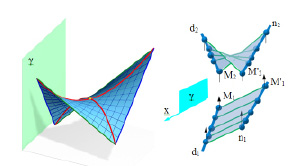
а б
Рис. 7.20. Параболоид гиперболический:
а – в пространстве; б – на комплексном чертеже
Поверхности с направляющей плоскостью называются косыми цилиндроидами, если обе направляющие являются кривыми линиями; косыми коноидами – если одна из направляющих – прямая линия; дважды косой плоскостью, если направляющие – скрещивающиеся прямые.
Дважды косой цилиндроид, как линейчатая поверхность с тремя направляющими, из которых две пространственные кривые и одна прямая показан на рис. 7.21.
На рис. 7.22. показан дважды косой коноид, образованный перемещением образующей прямой (красная) по трем направляющим, из которых две прямые. Показано построение одной образующей, как результата пересечения вспомогательной плоскости, проходящей через одну из прямолинейных направляющих, с двумя другими направляющими.
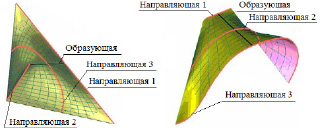
Рис. 7.21. Дважды косой цилиндроид
Рис. 7.22. Дважды косой
коноид
